04 Nov 1948

The Constituent Assembly of India met in the Constitution Hall, New Delhi, at Eleven of the clock, Mr. President (The Honourable Dr. Rajendra Prasad) in the Chair.

PRESENTATION OF CREDENTIALS AND SIGNING THE REGISTER.

The following Members presented their credentials and signed the Register:

(1) Shri H. Siddaveerappa (Mysore State);

(2) Mr. K. A. Mohammed (Travancore State);

(3) Shri R. Sankar (Travancore State);

(4) Shri Amritlal Vithaldas Thakkar [United State of Kathiawar (Saurashtra)];

(5) Shri Kaluram Virulkar [United State of Gwalior, Indore, Malwa (Madhya Bharat)];

(6) Shri Radhavallabh Vijayavargiya [United State of Gwalior, Indore, Malwa (Madhya Bharat)];

(7) Shri Ram Chandra Upadhyaya (United State of Matsya);

(8) Shri Raj Bahadur (United State of Matsya);

(9) Thakar Krishna Singh (Residuary States);

(10) Shri V. Ramaiah (Madras State);

(11) Dr. Y. S. Parmar (Himachal Pradesh).

TAKING – THE PLEDGE

The following Member, took the pledge.

Shri Syamanandan Sahaya.

HOMAGE TO THE FATHER OF THE NATION

Honourable Members, before we take up the items on the Order Paper, I bid you to rise in your places to pay our tribute of homage and reverence to the Father of the Nation who breathed life into our dead flesh and bones, who lifted us out of darkness of despondency and despair to the light and sunshine of hope and achievement and who led us from slavery to freedom. May his spirit continue to guide us. May his life and teaching be the torchlight to take us further on to our goal.

(All the Members stood up in silence.)

CONDOLENCE ON THE DEATHS OF QUAID- E-AZAM MOHAMMED ALI JINNAH, SHRI D. P. KHAITAN AND SHRI D. S. GURUNG

I ask you, Members, to stand in your places to pay our tribute of respect to Quaid-e-Azam Mohammed Ali Jinnah, who by his grim determination and stead fast devotion was able to carve out and found Pakistan and whose passing away at this moment is an irreparable loss to all. We send our heartfelt sympathies to our brethren across the frontier.

(The Members stood up in silence.)

Two Members have died since the Constituent Assembly met in its constitution – making function. They are Shri Debi Prasad Khaitan and Shri Damber Singh Gurung from Darjeeling. They represented their constituencies very faithfully and were of considerable help in our deliberations. I ask you to rise in your places to show our respect to their memory.

(The Members stood up in silence.)

AMENDMENTS TO CONSTITUENT ASSEMBLY RULES 5-A & 5-B

We shall now proceed to take up the items on the Order Paper. The first item is a motion by Mr. Govinda Menon and also by Shrimati Durgabai, of which notice has been given. I would ask Shrimati Durgabai to move it.

Sir, I beg to move:

That the provisions mentioned in the Constituent Assembly Notification No. CA/43/Ser/48-I, dated the 2nd August 1948, be made part of the Constituent Assembly Rules, as shown in the amendments below, with effect from the 2nd August, 1948: —     

(i) Rules 5-A and 5-B —     

For Rules 5-A and 5-B substitute the following Rule: —     

“5-A. When a vacancy occurs by reason of death, resignation or otherwise in the office of a member of the Assembly representing an Indian State or more than one Indian State specified in column 1 of the Annexure to the Schedule to these rules, the President shall notify the vacancy and make a request in writing to the authority specified in the corresponding entry in column 3 of that Annexure to proceed to fill the vacancy as soon as may reasonably be practicable by election or by nomination, as the case may be, in the case of the States specified in Part I of the said Annexure, and by election in the case of the States specified in Part II of that Annexure:    

Provided that in the case of the States specified in Part I of the said Annexure, where the seat was filled previously by nomination, the vacancy may be filled by election:    

Provided further that in making a request to fill a vacancy by election under this rule the President may also request that the election be completed within such time as may be specified by him.”    

(ii) In Rule 51 —    

“(b) ‘Returned candidate’ means a candidate whose name has been published in the appropriate Official Gazette as a duly elected member of the Assembly and includes a candidate whose name has been reported to the President in the manner provided in paragraph 5 of the Schedule to these rules as a duly chosen representative of any Indian State or States specified in column 1 of the Annexure to that Schedule.”    

(iii) In the Schedule —     

For paragraphs 3, 4, 5 and 6, substitute the following paragraphs:    

“3.(1) When the representation allotted to the States, individual or grouped in the Assembly, or the grouping of the States for the purpose of such representation is altered by an order made under paragraph 2, or by an amendment of the Annexure to this Schedule, the President may, by order —     

(a) re-assign members representing a State or States to such State or States as may be specified in the order;    

(b) declare the seat or seats of any member or members of the Assembly representing any State or States affected by an order under paragraph 2 or an amendment of the Annexure to this Schedule, as the case may be, to be vacant.    

(2) Any member who has been re-assigned to a State or States by an order made under clause (a) of sub- paragraph (1) and whose seat has not been declared vacant under clause (b) of that sub-paragraph shall as from the date of the order be deemed to be a duly chosen representative of such State or States.    

(3) A member whose seat is declared vacant by an order made under clause (b) of sub-paragraph (1) shall, if it is so specified in the order, continue to hold office as member of the Assembly until his successor has been duly elected and has taken his seat in the Assembly.    

4. (1) Not less than fifty per cent of the total representatives of the States specified in column 1 of Part I of the Annexure to this Schedule in the Assembly shall be elected by the elected members of the legislatures of the States concerned, or where such legislatures do not exist, by the members of electoral colleges constituted in accordance with the provisions made in this behalf by the authorities specified in the corresponding entries in column 3 of that Part.    

(2) All vacancies in the seats in the Assembly allotted to the States specified in column 1 of Part II of the Annexure to this Schedule shall be filled by election and the representatives of such States to be chosen to fill such seats shall be elected by the elected members of the legislatures of the States concerned, or where such legislatures do not exist, by the members of electoral colleges constituted in accordance with the provisions made in this behalf by the authorities specified in the corresponding entries in column 3 of that Part.    

5. On the completion of the election or nomination, as the case may be, of the representative or representatives or any State or States specified in column 1 of the Annexure to this Schedule in the Constituent Assembly, the authority mentioned in the corresponding entry in column 3 of that Annexure shall make a notification under his signature and the seal of his office stating the name or names of the person or persons so elected or nominated and cause it to be communicated to the President of the Assembly.”

Sir, before I commend my motion to the House for its acceptance, I wish to say a few words of explanation as to why and how these amendments to the rules have become necessary.

Sir, Rules 5-A and 5-B of the Constituent Assembly Rules lay down the procedure for filling a casual vacancy in the office of a member representing an Indian State or more than one Indian State and the Schedule to the Rules prescribes the allocation of seats in the various States or groups of States and the manner of choosing the States representatives and also the method of appointing conveners for purposes of conducting election. These Rules 5-A and 5-B were based on conclusions reached by the two Negotiating Committees set up by the Chamber of Princes and also by the Constituent Assembly.

Sir, since then, as it is common knowledge, many changes of a far-reaching character have taken place and these changes have taken place both in the constitutional as well as in the administrative set up of these states. For example, certain States have formed themselves into Unions and certain others have merged into neighbouring provinces and still certain others have been constituted into Centrally Administered Areas.

Sir, these changes in their turn affected radically in the case of some the existing scheme of representation in the Constituent Assembly. Consequently, it became necessary to re-group these several States and to re-allocate seats among them and also change the conveners for the purpose of conducting elections and also make necessary changes in the rules of the Constituent Assembly. All these matters were considered at a meeting of the Honourable the President and of the Honourable the Minister of States and also the Rajpramukhs and the Premiers of the Union and the States concerned and also the Premiers of various provinces affected by these changes and also of the officials of the Secretariat of the Constituent Assembly and of the States Ministry; and the decisions reached at that Conference are now embodied in these provisions which are now sought to be incorporated in the Constituent Assembly Rules.

Now, Sir, the most important feature of these changes in the provisions is that in the case of newly formed group or Union of the States – Cutch and Junagarh, which have been given separate representation in the Assembly – all the vacancies in the seats are to be filled by election by the elected members of the Legislatures of the States or where such legislatures do not exist, by any other Electoral College which is set up for that purpose.

Under the old Rules some of them could be filled by nomination. Sir, as you have already noted the various changes, I do not think that I need elaborate these points. I commend my motion to the House for its acceptance. Sir, I move.

I have received notice of certain amendments to this motion. Mr. Kamath.

Mr. President, Sir, I move:

“That in sub-para, (1) of the proposed paragraph 3 of the Schedule, for the words ‘to the States, individual or grouped in the Assembly’ the words ‘in the Assembly to the States, individual or grouped’ be substituted.“

That is to say, if the amendment is accepted, it will read thus: Now it reads, “When the representation allotted to the States, individual or grouped in the Assembly“. In the place of this, it will read, “When the representation allotted in the Assembly to the States, individual or grouped…..” I do not think I need speak much on this amendment. It is self evident and the meaning that is sought to be conveyed by the paragraph is as represented in my amendment. Certainly, the States individual or grouped as they are, is not for Assembly purposes. Therefore, it should be “representation allotted in the Assembly to the States, individual or grouped.” This is the first amendment.

Sir, the second amendment runs thus:

“That in sub-para. (3) of the proposed paragraph 3 of the Schedule, for the words ‘is declared vacant’ the words ‘has been declared vacant’ be substituted.“

This is purely, if I may say so, a linguistic amendment. I think it refers to the state of affairs arising after a seat has been declared vacant. The wording “when a seat has been declared vacant” is more correct and more accurate.

I therefore commend these amendments of mine for the acceptance of the House. Sir, I wish to speak on the motion. May I speak?

Yes.

Sir, I seek some clarification on certain points that have arisen from the motion moved by my honourable friend Shrimati Durgabai. Sir, the potential strength of this Assembly is 324. I am given to understand that the actual strength today is 303. Twenty one members who are to represent Hyderabad, Kashmir and Bhopal are not present with us. Even as regards the remaining 303, the papers yesterday brought us the news that the Patiala and East Punjab States Union have not elected their representatives to this Assembly. I do not know why these States or Union of States or groups of States should continue to be unrepresented in this last and most important session of the Constituent Assembly. As regards Kashmir I agree there are difficulties. As regards Hyderabad which now forms one of the States specified in Part I of the Annexure, it takes top rank among the States. I do not see why we should not call upon the Ruler of Hyderabad or to elect or to elect and nominate as the case may be in accordance with the provisions of this resolution, and send representatives to take their place in this Session as early as possible. In view of the recent events that have taken place, a happy denouement–I hope the House is in agreement with me that we have had a happy termination of the Hyderabad episode–we wish to welcome our friends, our colleagues from Hyderabad as soon as possible in this Assembly. As regards Bhopal, I do not know what difficulties stand in the way, what stumbling block there is in the way, what obstacle has to be surmounted, so far as the participation of Bhopal in this Assembly is concerned. I would plead with you and I would request that the Bhopal authorities should also be called upon at once to send their members to this Assembly with the least possible delay.

Then, Sir, the report which appeared in the press yesterday as regards Patiala and East Punjab States Union was not very clear. It alleged all sorts of things against the administration and against the Ruler; but, whatever it may be, I think it is high time that this Union of Patiala and East Punjab States should be called upon to send their representatives to this last session of the Constituent Assembly.

There is another point which I would like to draw your attention to. In the Rules that have been framed by us during the previous sessions. We have stated-I refer to Rule5 sub-rule (2)– “Upon the occurrence of a vacancy, the President shall ordinarily make a request in writing to the Speaker of the Provincial Legislative Assembly concerned, or as the case may be, to the President of the Coorg Legislative Council, for the election of a person, for the purpose of filling the vacancy as soon as may reasonably be practicable.” Here, now that in some of the States mentioned in Part I of the Annexure–I am sorry I cannot say off hand which States have got elected legislature functioning–take for instance, Mysore; it is a big State and it has already sent its representatives to this Assembly–so far as such States are concerned, I see no reason why in future, instead of the Ruler, the Speaker or President of the Assembly should not be requested to fill the vacancies that may arise. It may be argued against this that the Rule as it stands, 5-A provides for the Ruler being the authority in this case. But, as we are amending the Rules, why not amend certain provisions of these Rules so as to make them more in conformity with democratic practice and democratic traditions? Therefore, I would ask my honourable friend Shrimati Durgabai to explain why, in the case of those states where we have got Assemblies functioning, the Speaker or the President should not be the authority instead of the Ruler. On this point, I would ask some more light from the mover of the motion.

Sir, before I resume my seat, I commend my two amendments to this motion for the acceptance of the House. Thank you, Sir.

Mr. Sidhwa.

Mr. President, Sir, my amendment was–

“That in sub- para. (1) of the proposed paragraph 4 of the Schedule, delete the words ‘Not less than fifty per cent’ of and for the words ‘the total representatives’ the words ‘The total number of representatives’ be substituted.“

The object of my amendment was that while we have done away with the nomination system in our Constitution, it would not be fair to allow the States, particularly the Rulers to nominate the 50 per cent. I therefore, with that object in view and just in conformity with our decision for abolishing the nominations, suggested the abolishment of this also. I however understand that an arrangement has been arrived at between the Rulers and the people of the State and the States people have agreed to this arrangement being continued and I am also told that although this is there, the representatives are all elected by the people themselves. If that is so as I understand it is so, I do not propose to move this amendment.

Do you move the amendment or not?

I do not move it, Sir.

All the amendments of which I have notice, so far as this motion is concerned, have been moved. I have received a complaint from one Member that the agenda and amendments have been circulated here and he did not get them before and so he has not been able to give notice of amendments and he wants that the discussion be adjourned. I understand from the Secretariat that the agenda and other papers were circulated some days ago but they were sent to the addresses that were then known to the office and it is possible that the Members during the course of transit have not been able to get the papers that were sent to them and by way of caution a second copy has been supplied here today. It is not as if the agenda and the papers have not been circulated. Only the second copies have been given today. I do not think there is any ground for adjourning the discussion of this motion particularly because after all it is more or less a motion of a formal nature, because we have already acted upon these Rules and they are not likely to be acted upon in the future when this session of the Assembly is over.

*[ I have no objection in complying with your order. But I submit that the information supplied to you by the office is incorrect. Many of the Members have not received copies of the agenda. Not I alone but two or three of my colleagues also who are present here have not received it. I am in greater difficulty as my telephone has also been disconnected even though they had already taken from me the subscription for the whole year. Twice I have referred this matter to the Deputy Minister for Communications but telephone connection has not yet been restored. When I came here I telephoned from another place to the Deputy Secretary, Constituent Assembly, and informed him that no copy of the agenda had been received by me and that the telephone connection also had not been restored. This is the situation of the Members and I would like to make my protest against it. Had it been so with me alone, you could have adopted this course. But there are many Members present here who have not received the agenda. The Deputy Minister ShriKhurshedLalis also one of them. He also denies having received a copy of the agenda. I don’t know how it was circulated but even he complains of not having received it. Twice I complained to him that my telephone connection had not been restored even though the subscription money had been realised by them for the whole year. You have reduced us Members to this miserable plight. As for the agenda, I am not the only Member to complain about it. Many Members have not received it. There are important items on the agenda and as a protest I demand the postponement of its consideration.]

*[Copies of the agenda were sent to the Members by the office. Whether it did reach the Members or not is a matter for Shri Khurshed Lal to answer. It is also his responsibility to see whether telephone connections have been provided or not. I do not think that there is any important reason to adjourn the House. If any Member wants to speak on this matter he may do so.]

*[ I would like to suggest that you are empowered to admit the amendments which are, even now, received from Honourable Members. That would leave no room for grumbling.]

*[ As I have not received any amendment as yet, the question does not arise.]

*[Mr. President, I request that these amendments which have been moved should be considered if they need consideration. But first of all a chance should be given to the mover…]

*[ Had I received any amendment I would have allowed it to be moved in the House. But no amendment has been received. Now, you want that this discussion should be postponed so that there might be an opportunity to move an amendment. But as yet I have no amendment before me.]

*[ Mr. President, in this connection, it is submitted that your orders are binding on all. If the copy of the agenda is lost in transit the purpose of sending it–, and it is that the Members may go through it and may form their opinion—is defeated. Consequently if it could not reach the Member or if there is any delay or error in its despatch from the Assembly office, and thereby if any Member did not receive the agenda, then in my opinion it requires consideration whether the resolution may be taken up for consideration on that day or not. I want to draw your attention to this fact.]

*[I do not think it necessary at this stage, for such questions are not before us as require prolonged discussions and postponement of the debate to some other day and stoppage of our proceedings today.]

Mr. President, Sir, I do not have to make the complaint that some of the honourable members of this House have made, although I must say that I did not get the agenda before yesterday, and that is the reason why it was not possible for me–my stenographer not having arrived–to send  in my amendment to the various Rules. It is quite clear that the Rules are pretty lengthy and therefore the amendments are also likely to be of a similar nature. I hope therefore that you will kindly pardon my not having sent in my amendments and the few amendments that I propose would be considered by the Honourable Mover of the Motion. The first amendment I would suggest is—

“In the first part of Rule 5-A instead of ‘an Indian State or more than one Indian State’ substitute the words ‘one or more Indian States’.“

I personally think it is better English in that way. My second amendment is–

“Instead of the words ‘make a request’ the word ‘direct’ be substituted.“

It should be possible for you Sir, to direct the authorities specified in the corresponding entry in column 3 of that Annexure. I do not think it is in consonance with the dignity of the office you hold or the position of this Constituent Assembly that it should be necessary to request a petty State or the Authority existing therein to hold the elections. We, as Members of the Constituent Assembly are summoned by you. I would therefore suggest the adoption of the above amendment.

Similar words are used in the second proviso. There also the word ‘request’ has been used. That also should be changed to ‘direct’.

There is also one more amendment I would suggest so far as the second proviso is concerned. I suggest that–

“The proviso as it stands be substituted by the following, viz. ‘Provided further that in directing to proceed to fill a vacancy by election under this Rule the President may also direct that the election be completed by a certain date’.“

The change is to replace the words “making a request to fill” by the words “directing to proceed to fill“. The word “request” is changed into “direct“, and the concluding words–‘within such time as may be specified by him’–are proposed to be changed by the words “by a certain date“.

The wording in paragraph 3 (1) on page two may read better if it were put as follows:

“When the representation allotted to any States, jointly or individually, in the Assembly or the grouping of the States for the purpose of such representation is altered by an order made under paragraph 2, or by an amendment of the Annexure to this Schedule, the President may by order–……………..“

The alteration would be to change the word “the” into “any“, and to omit the words “individual or grouped in the Assembly“, by merely saying “jointly or individually“.

This amendment of mine is very similar to the one moved by Mr. Kamath. I think he was somewhat hesitant in suggesting a wholesale alteration of the clause. That is why the suggestion he has made, although it has the same intention, does not express it so correctly as the suggestion made by me. I Hope, Sir, it will be possible for the honourable Mover to consider the various amendments suggested by me, and if possible to accept them. 

Sir, I have just given notice of an amendment. Before moving it I would like to explain the position as it is today. 

In part 1 to the Annexure, Mayurbhanj State has been mentioned with one representatives and the Returning Officer is the Ruler of Mayurbhanj. But it has been decided by the States ministry that the State of Mayurbhanj can not stand singly by itself and it has been agreed that it shall merge into the province of Orissa, along with the twenty-three other States that have already merged.

Has the Mayurbhanj State already merged or is it a proposal? 

I believe they have signed a certain agreement and they are going to hand over the State to the Government of India and that an Administrator has been already appointed and that he is going to take charge of the State. Under these circumstances, I believe there is no justification for treating Mayurbhanj State as a separate identity, and again to recognize the Ruler of Mayurbhanj State as the Retuning Officer. I do not know, and I can not say whether the Government of India have actually intimated to the Government of Orissa that Mayurbhanj State is to merge in Orissa. But this much I can assure you, and through you the Honourable Members of the Constituent Assembly that this is expressed view of the Government of India that it shall be merged into the province of Orissa. Therefore, there is absolutely no purpose in bringing in something which will undo what has been already done and decided by the States Ministry with the full concurrence of the State of Mayubhanj, the people and also the province of Orissa. 

Therefore, Sir, I beg to move an amendment, which is (I have given notice of it just now.):

“Omit Mayurbhanj with its representation of one and the Ruler of Mayurbhanj as the Returning Officer from Part 1 of the Annexure.“

I further move:

“That the State of Mayurbhanj be added to the Orissa States in Part II of the said Annexure, substituting 24 for 23 and also under the column of representation substituting 5 for 4, including 1 from the Sate of Mayurbhanj, and the Governor of Orissa to continue as the Returning Officer.“

This is the complete amendment that I place before the Honourable Members of the Constituent Assembly and think that it is a necessity.

If you propose to give separate representation and a separate identity to Mayurbhanj, that means you propose to perpetuate the independent existence of smaller States, a policy which has been refuted and not accepted by the States Ministry and the Government of India. Therefore, my amendment is just to give effect to the very idea which has been accepted, adumbrated and followed in principle and in practice by the States Ministry and the Government of India. 

I may point out to Members that as the States are concerned, the question has been in a state of flux. There have been so many changes going on from day to day that it has been difficult to keep pace with them. The proposal is based upon the recommendation of the States Ministry, and the proposal was reached at a conference at which not only the Prime Ministers of all the provinces concerned but also of the Sates concerned and Rajpramukhs were present, and there were representatives of the States Ministry as also of the Constituent Assembly, and these proposals are in conformity with recommendations of that Conference. If there has been any change since then, we have no notice of that change. Besides, there will be no difficulty in altering any of the rules subsequently if a change has taken place. So I would suggest toShriBiswanath Dasthat he need not apprehend that there is any question of perpetuating smaller States. At the moment we are proceeding upon facts that we know and we are recognizing those facts and making the rules in conformity with those facts. As soon as a change in those facts takes place, and we are informed of that change, we shall change the rules accordingly. So I would suggest to him not to press his amendment at this stage. We can take up the matter as soon as the States Ministry is in a position to tell us that this ought to be changed. 

An officer of the States Ministry is here. These are the salient facts. I do not dispute them but I beg of him not to dispute the facts that I have placed before him.

I do not dispute his facts. I only say that I have received no intimation from the States Ministry to that effect and therefore we are proceeding upon what we have from the States Ministry. As soon as we have information, there will be no difficulty in changing the rules. That can be done at any sitting. 

You are going to take charge of the State. The moment newspapers published that the Constituent Assembly has given separate representation to the State I assure you that there will be tremendous trouble to be faced not by me or the people of Orissa but by the very administrator that is going to be appointed by the Government of India. Under these circumstances I appeal to you, knowing as you do the difficulties of the situation and as a person having an intimate knowledge of the areas and the people concerned, not to tread on dangerous ground. I do not want to press my amendment. I have only brought this matter to your notice as also to the notice of the Constituent Assembly. 

I think the newspapers will not only publish the fact that Mayurbhanj has been given separate representation but also the statements which I have made and you have made. Along with these statements the information itself will have no effect of the kind that you apprehend and I would therefore suggest to the honourable Member not to press his amendment.

*[ Mr. President, I would like to know if an amendment which is contrary to the principles accepted by the Negotiating Committee can be moved to the amendment now before us. For example, 50 per cent is fixed in it. Is it possible to move an amendment that instead of 50 per cent. All the members should be elected or that they should be nominated by the Raj Pramukhs or that the members must be elected on the basis of the electoral rolls that had been prepared before in the States? I would like to know whether an amendment can be moved which goes beyond the principles accepted by the Negotiating Committee.]

I think we have to be very cautious in dealing with the States. We are proceeding on the basis of the agreements entered into with the States and here we should not say or do anything which may have the effect of going back upon any agreement which has been made with the States. All these amendments are based upon agreements which have been made between the States Ministry and the States concerned. The House will remember that originally there was one set of agreements but that has become out of date and therefore we have a second set of agreements. All these amendments are based upon these agreements and I would therefore suggest that nothing should be done to go back upon any of the agreements that have been entered into.

I would ask Mr. Sidhwa not to press his amendment….

He has not moved it.

Sir, I beg leave of the House to move the amendment of which I have given notice just now. I am in agreement with the original motion but as regards the Annexure Part I, third Column (viz. Authority for the purpose of the choosing of representatives in the Constituent Assembly) I propose to move an amendment to the word Ruler of Hyderabad, Mysore, Kashmir and so on. I would like to say that the rulers today do not have the real ruling power, as it has been transferred to the people of the State, especially since August 15th 1947. So, Sir, I think the ruler of any State should not be made the authority for the purpose of choosing representatives in the Constituent Assembly, as he has not got the authority to choose. What is the good of calling someone an authority who really has not got that authority? To me it does not look to be in order. I shall be thankful if the Honourable the Mover accepts my amendment:

“That for the word ‘Ruler’ in column 3 of annexure Part I the word ‘people’ be substituted.“

If you find that this is not in order then for instance, the Speaker of any Assembly, which has been elected by the people of that State, occupies a more important place than that of the Ruler. No doubt the Ruler is there as a nominal figurehead but the real person who rules is either the prime Minister or the Legislative Assembly, wherever there is one. So, Sir, I would request that the Honourable the Mover would accept this simple amendment. I have proposed a simple amendment and I need not explain it further. I hope the House will be good enough to accept it.

I might point out that the Honourable member’s amendment is wholly misconceived. It is not as if the Ruler is going to nominate the representatives. The Rulers have to be addressed for the purpose of getting the representatives elected by the bodies who have the right to elect them. The Ruler does not come in in any other way. 

That is exactly my point. You are addressing the Ruler but the Ruler has not got any authority to elect. What is the good of asking a person who does not possess the power? The actual power is not with the Ruler but with the people of the State. So the representatives should be elected by the people of the State–either the Speaker of the Assembly wherever there is an Assembly functioning or the Prime Minister or the Raj Pramukh who has been duly elected. They will be the proper authority. Even for the sake of form it should not be there. 

I have pointed out the position to the Honourable Member but if he wants to press his amendment…… 

There is no question of pressing the amendment. I have understood, Sir, your point. You have been kind enough to enlighten me that the ruler is only a figurehead and is meant for the purpose of addressing someone. But what I say is, what is the good of addressing a Ruler who has not got the authority and who has transferred his authority to the people of the State?

Every order of the Government of India also goes in the name of the Governor-General, although it is the Ministers who pass the orders. The position is exactly similar. 

Sir, I accept your advice and I leave it to you.

Mr. President, I do not think I have much to say by way of replying to the points raised by several Honourable Members of the House and I am thankful to you, Sir, that you had taken upon yourself the task of explaining some of the points raised by the Honourable Members. I would not refer to the points raised by Shri Biswanath Das and Shri Nagappa, because the Honourable President has sufficiently dealt with those points.

With regard to the amendment moved by Dr. P.S. Deshmukh, I think the existing expression, ‘make a request in writing’ is more happily worded than that suggested by him and is also very courteous, I do not think there is need for a change. His other amendment also I cannot accept for the same reason.

With regard to the point raised by Mr. Kamath in his amendments, I may say that I appreciate it and have great pleasure in accepting his amendments. They are really verbal amendments and I accept them.

He has raised the question of Hyderabad and Kashmir in this connection. I do not think it is for me to say any thing on the points he has raised about those States; but I feel that those points are irrelevant to the motion I have moved here. I commend my motion to the House for its acceptance.

Mr. President, I have not moved any amendment and therefore the question of irrelevancy does not arise, I only wanted to know whether Hyderabad, Bhopal and Kashmir would send their representatives to the Assembly. I only wanted some light and clarification on the point.

I shall put the amendments to vote. The amendment of Mr. Kamath runs thus:

“That in sub- Para (1) of the proposed paragraph 3 of the Schedule, for the words ‘to the States, individual or grouped in the Assembly’, the words ‘in the Assembly to the States, individual or grouped’ be substituted.“

This has been accepted by the Mover. 

The amendment was adopted.

The other amendment of Mr. Kamath, viz.,”That in sub-para. (3) of the proposed paragraph 3 of the Schedule, for the words ‘is declared vacant’ the words ‘has been declared vacant’ be substituted” is now for the vote of the House.” This has also been accepted by the Mover.

The amendment was adopted.

Then there are the amendments of Dr. Deshmukh. So far as the wording of one of them at any rate is concerned, it has been already accepted when Mr. Kamath’s amendment was accepted. The other amendment is only a question of taste whether we should make a direction or a request. As Dr. Deshmukh has not withdrawn it, I shall put it to vote. The amendment is:

“In the place of the word ‘request’ the word ‘direct’ should be used.“

The amendment was negatived.

I shall now put the amendment of Dr. Deshmukh to Clause 3(i) of the Schedule to vote.

The amendment was negatived.

The amendment of Mr. Biswanath Das was, by leave of the Assembly withdrawn.

Shri S. Nagappa’s amendment was, by leave of the Assembly, withdrawn.

The motion, as amended, is for the vote of the House.

Would you please tell us whether Hyderabad and Kashmir would send their representatives to this Assembly?

I am not in a position to give any information on that point. The Government, if they liked, would have given you the information by now. The motion, as amended, is for the vote of the House.

The motion, as amended, was adopted.

AMENDMENT TO THE ANNEXURE TO THE SCHEDULE

Srimati Durgabai may now move her second motion.

Mr. President I beg to move the following motion :

” That the provisions mentioned in the Constituent Assembly Notification, No. CA/43/Ser/48-II, dated the 3rd August1948, be made part of the Constituent Assembly Rules, as shown in the amendments below, with effect from 3rd August 1948.”

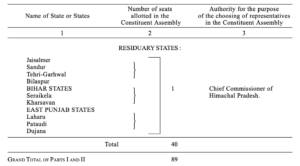
For the Annexure to the Schedule substitute the following Annexure :-

ANNEXURE

Part I

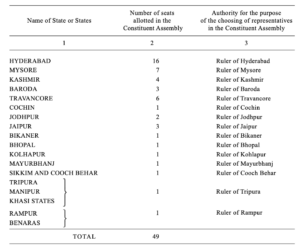
Part II

Part II – contd.

Part II – contd.

Mr. President, the amendment I have given notice of is an extremely simple one and a purely verbal one intended to add the definite article ‘the’. It reads:

“That in part II of the proposed Annexure to the Schedule, for the words ‘Governor of Central Provinces and Berar’ in the 3rd column under the heading ‘Central Provinces and Berar States’, the words ‘Governor of the Central Provinces and Berar’ be substituted.“

I would invite your attention and the attention of the House to the name by which my province is known in official documents and records. In our draft Constitution, of which we have all got copies in Schedule I, Part I, page 159 where the list of the various provinces has been given, and you will find my province described as the Central Provinces and Berar.

I do not want you to adduce arguments in support of this amendment. 

I move the amendment and commend it for the acceptance of the House.

Do you accept that?

I accept that.

The amendment is that the word “the” be added before the words “Central Provinces and Berar“.

The amendment was adopted.

The motion, as amended, is now put to vote. 
 

The motion, as amended, was adopted.

Addition of New Rule-38-V

Sir, I beg to move that the following amendment to the Constituent Assembly Rules be taken into consideration:

After rule 38-U insert the following-

“38-V. When a Bill referred to in Rule 38-A is passed by the Assembly, the President shall authenticate the same by affixing his signature thereto. When the Bill is so authenticated it shall become an Act and shall be published in the Gazette of India.“

Sir, before I commend my motion for the acceptance of the House, I consider it my duty to offer a few words of explanation as to why this amendment has become necessary. Sir, I am sure that Honourable Members are aware that during the last session of the Constituent Assembly when it met on the 27th January, certain amendments were proposed and accepted by this House to the rules of the Constituent Assembly, and one of those amendments was to introduce a new rule 38-V laying down the procedure for passing of the Bills referred to in Rule 38-A. Sir, that proposed rule 38-V raised a good deal of controversy and objections were raised by some Honourable Members on the ground that a Bill passed by the Constituent Assembly for amending the Indian Independence Act or the Government of India Act 1935 as adapted by that Act should not be subject to the assent of the Governor-General since such a procedure might detract from the sovereign character of the Assembly. Another objection was raised on the ground that, if that rule was adopted, the consequence would follow that the Governor-General might give or withhold his assent even to a Bill seeking to amend the existing constitution. Another objection was raised on the ground that there should not be any difference between the procedure to be adopted for passing the Draft Constitution and for passing a Bill seeking to amend the existing Act. These objections were discussed and after prolonged discussion, the suggestion made by Mr. Kamathto refer the proposed rule back to the Draft Committee for re-examination in the light of the objections raised, was accepted. This suggestion was accepted by the House and the rule was referred back to the Drafting Committee. The Drafting Committee has considered this rule and their fresh proposal is before the House. Sir, this new rule dispenses with the ascent of the Governor-General to any Bill passed by the Constituent Assembly under Rule 38-A. The original rule reads thus:

“When a Bill referred to in Rule 30-A is passed by the Assembly, a copy thereof signed by the President shall be submitted to the Governor-General for his assent. When the Bill is assented to by the Governor-General, it shall become an Act and shall be published in the Gazette of India.“

I think Members have understood the significance of the change proposed and that I need not elaborate this point. I commend my motion for the acceptance of the House.

Mr. Kamath has tabled an amendment to this to substitute the words “has been” for the word “is“.

Sir, I move:

“That in the proposed rule 38-V for the words `when the Bill is so authenticated’ the words `When the Bill has been so authenticated’ be substituted.“

This amendment, Sir, is entirely similar to the one which has been accepted by the House with regard to another motion moved by my honourable Friend. Mrs. Durgabai. I think it will be happier and more in consonance with the rules of idiom and usage to substitute the words “has been” for the word “is” so that, if the amendment is accepted, the proposed rule will read:

“When a Bill referred to in rule 38-A is passed by the Assembly, the President shall authenticate the same by affixing his signature thereto. When the Bill has been so authenticated, it shall become an Act . . . .” etc.

I commend this amendment for the acceptance of the House.

The motion has been moved and also an amendment to that. If any Member wishes to speak on the motion, he may do so now.

I accept the amendment.

It seems there is nobody who wishes to speak on the motion. The mover has accepted the amendment. I first put the amendment to vote.

The amendment was adopted.

The motion, as amended, is now put to vote.

The motion, as amended, was adopted.

PROGRAMME OF BUSINESS

We will now go on to the next item on the agenda but before doing so, I would like to explain to the House the procedure which I propose to follow in dealing with the Draft Constitution. Members are aware that the Draft Constitution was prepared by a Drafting Committee which was appointed by this House and the Draft was placed in the hands of Members nearly eight months or more ago. Members were asked to send in any suggestions or amendments which they wished to make and a large number of suggestions and amendments were received not only from Members but also from the public and public bodies, provincial governments and so forth. The Drafting Committee has considered all these suggestions and amendments and they have redrafted many of the articles in the light of the suggestions made by either Members or the public. So we have now got not only the Draft as it was originally prepared, but also the re-draft of a number of the Articles which the Drafting Committee had prepared in the light of suggestions received. These have been placed in the hands of Members. What I propose now to do is to take up each Article after we, of course, have passed this motion for consideration and I shall take all these amendments of which notice has been given already as having been given in time, so that Members who have already given notice of amendments need not repeat the notice after the motion for consideration has been adopted. I will also give to Members two days more forgiving notice of any further amendments which they wish to propose to the Articles. And then, I propose not to accept any other amendments, unless they are of such a nature that it becomes necessary to accept them. Of course, there will be amendments which may be consequential and those will have to be accepted. There may also be amendments which for other reasons may be considered by the House to be of such a nature that they should be considered; I will not burke  discussion of those amendments; I shall have them also. But ordinarily I would ask the Members to confine themselves to the amendments of which we have already got notice and they are, I believe, about a thousand in number. In this way we might economise time without in any way affecting our efficiency and without in any way putting any check on free discussion of all the Articles of the proposed draft. This is what I propose to do, of course, subject to what the House lays down. I think this is quite reasonable in view of the fact that Members have had such a long time to consider; and that they have considered in detail the draft is apparent from the fact that we have already got notice of about a thousand amendments, and if by any chance any amendment has been overlooked and if any member feels its consideration to be necessary, we shall take it, but ordinarily I will not take any further amendments after this. What I propose is that we discuss the motion, which Dr. Ambedkar will move, for two days, that is, today and tomorrow, when we sit both in the morning and in the afternoon and we give Saturday and Sunday for giving notice of amendments to the members. All the amendments of which we have already received notice and of which we shall have received notice by 5 o’clock on Sunday will be tabulated, printed and placed in the hands of Members by Monday, and then we proceed with the discussion of the amendments from Tuesday. That is the programme which I have outlined in my mind.

There is another thing which I might tell Members. There is a motion of which notice has been given and there is also an amendment of which notice has been given that this House should adjourn discussion of the Constitution altogether and a new House on adult franchise and on non-communal lines should be elected and that House should deal with the question of framing the Constitution. I do not know if the House will be prepared to throw away all that we have been doing during the last two years, particularly because there is in the Draft an article which gives a somewhat easy method of amending the Constitution during the early years after it comes into force and if there is any lacuna or if there is anything which needs amendment, that could easily be done under the provision to which I have just made reference, and it is, therefore, not necessary that we should hold up the consideration of the entire Constitution until we have adult franchise. The difficulty will be in the first place to form the electorate under adult franchise; we have no such law existing at present. Adult franchise we have contemplated in this Draft Constitution and it will come into force when this Constitution has been passed. So if you want to have adult franchise and if you want to have another Constituent Assembly for the purpose of drafting the amendments, we shall have to pass another law and I do not know which House will have the right to pass that law which will constitute a Constituent Assembly. So I think it would be best to proceed with the draft which we have prepared after much labour and to which so much care and attention has been given by the Drafting Committee and by the Members of this House.

This is the programme which I propose to follow and if there is any other suggestion which any member wishes to make, I shall be glad to consider it. There is only one thing more which I might mention and that is this. I do not wish to curtail discussion. I want to give to members the fullest opportunity for considering every article and every aspect of the Constitutional question, because, after all, it is going to be our Constitution, but at the same time, I do not like that we should spend more time than is absolutely necessary over it by repeating arguments which have already been once advanced by one Member or another or by going over the same ground. For that reason, we may not reconsider many of the decisions which have already been taken. Members know that we had long discussions, and after long discussions we settled the principles of the Constitution and the Draft, the bulk of it, is based upon those decisions which were taken after long discussion by this House. I would not expect that the Members would lightly throw away those decisions and insist upon are consideration of those decisions. There may be cases where a reconsideration may be necessary. But ordinarily, we shall proceed upon the decisions which have already once been taken and it is only where no decisions have yet been taken that the House may have to take decisions for the first time. Now there are certain questions on which no decisions have been taken. There were certain committees appointed by the House. The reports of those Committees were not considered. But the Drafting Committee has taken care to place in the draft alternative proposals, one set of proposals representing their own views where they differ from those of those Committees and another set of proposals embodying the recommendations and the decisions of those Committees. So when we come to those particular provisions, the House may consider them on their merits, and after considering them on their merits may accept either the opinion of the Drafting Committee or of the Committee. The House will have the draft ready, so that it will not have to wait for preparing a draft on these questions. When we consider this whole matter from this point of view, I think, after all, the scope for discussion gets very much limited, because most of the amendments will be more or less of a drafting nature, because the decisions have already been taken, and so far as the drafting is concerned, the Drafting Committee has already considered many of these suggestions and amendments and it has accepted them. So, while there maybe discussion of principle in regard to some questions which have not been decided, there is not much to discuss so far as principles are concerned, because we have already discussed those principles and we have arrived at certain conclusions. Therefore, what I feel is this, that if we proceeded in a business-like way, it should be possible for us to complete discussion of the whole Constitution by the second anniversary of the day on which we started the work of this Constituent Assembly, that is, by the 9th of December next.

If we succeed in doing that, after that we might have a few days adjournment, when all the amendments which have been accepted by the House will be considered by the Drafting Committee and put in their proper places, when all the re-numbering and re-allocation of the Articles from one Chapter to another and so forth–all that becomes necessary–all that could be done within that interval of say ten or fifteen days. Then, we might meet a second time when we could finally accept the Constitution as it will have emerged. In this second discussion, under the Rules, we shall not go into the merits of any question; we shall have only to see that the amendments as they were accepted by the House have been incorporated in the final form in which the draft is placed before the House.

This is the proposal which I place before the House and I think this ought to meet with the approval of the members of this House.

*[Mr. President, I would like to know whether after adoption of the article relating to the national language, clauses which might have been passed by then in English would be placed before this House for adoption in Hindi.]

*[Yes, of course, all the clauses would be reconsidered in that language which may have been adopted as the national language. There would be no discussion at that time on the clauses as such. The only point for consideration would be whether the clause has been correctly translated or not. I, therefore, think that our discussions should be based on the English draft at present, for all those who have given thought to the draft and those who have prepared it, have done so in that language only. And when clause relating to the national language is finally adopted we would put up the translation of the Constitution in that language before you for adoption.]

Sir, I wish to draw your attention to this very important question which my honourable friend Seth Govind Dashas raised before the House.

*[Mr. President, I would like to submit that before we proceed to discuss fundamental questions, it appears desirable that you should decide what the procedure would be for tabling amendments. Shall the old procedure be followed or the one which you have stated now? It is necessary so that we may have some idea of the order in which debate would proceed, and the time we would be allowed for sending in amendments.]

*[Both will be decided simultaneously.]

Sir, I fail to see where the point of order lies. As a matter of fact, I only wanted to draw your attention to one thing. Before you call upon the Honourable Dr. Ambedkar to move that the Draft Constitution be taken into consideration, I should like to draw your attention to the question which has been raised by my friend Seth Govind Das. After the motion which the Honourable Dr. Ambedkar is to move has been carried, we shall certainly consider the Constitution clause by clause. As you know, Sir, I am one of those who had given notice that the National language of India be Hindi and the script the Devnagari script. Naturally, the question will arise when we take into consideration one clause after the other of our Constitution, as to which language will it be in which the Constitution shall be deemed to have been passed. My suggestion, therefore, before you will be that when we consider the clauses of the Constitution, after finishing one Chapter of it, we must revert in Hindi and pass every clause as has been amended by this House and as has been translated in that language by a Sub-Committee of this House. I would therefore request you, Sir, that before you take up the consideration of the Constitution clause by clause, you may be pleased to appoint a Sub-Committee of this House which will keep itself in touch with the clauses and the amendments that the House wishes to make therein and as they are passed, and that Committee should get these clauses translated and these clauses, after finishing one Chapter, may again be brought before the House in Hindi and it could be deemed to have been passed in Hindi also. So that, after some time, when we have ultimately done away with the English language, the original must be considered to have been passed in Hindi, and it should be the ultimate authority, the authentic constitution. If we do not adopt any such course, I think we shall be greatly handicapped at the time when I think article 99 of the Constitution comes before us and we declare our language as Hindi and the script the Devnagari script. I think there is some difficulty before my South Indian friends. They can easily say that “this Constitution at present is in the English language which we all understand, you call upon us to pass every clause in Hindi, and we do not know the language.” I think those of my South Indian friends who do not know Hindi to such an extent may rely on the better sense of their colleagues. Here, in this House, there are friends who do not know English and yet they rely upon your good sense and they do not raise the objection that they do not know the English language and therefore this Constitution is not good. Similarly, they may try to accommodate us in this matter.

I think it will cut short discussion on this point if I explain what I propose to do in regard to this matter. There is a motion of which notice has been given that a Committee should be appointed for the purpose of preparing a translation and that translation should be passed Article by Article by this House, and that should be treated as the original. There is something to that effect of which notice has been given. What I propose to do is this. Members are aware that we have got translations prepared: there is a translation in Hindi; there is a translation in Urdu; there is a translation in Hindustani; all these three translations of the Draft Constitution are ready and I believe members have received copies of these translations. As soon as the question is decided as to what will be our language, we shall set up a Committee which will take up that particular translation which is ready and see to it that it conforms literally to the original in English. Whatever our sentiments may  dictate, we have to recognise the fact that most of those who have been concerned with the drafting of the constitution can express themselves better in English than they can in Hindi; it is not only a question of expressing in English or Hindi, but the ideas have also been taken from Constitutions of the West. So the expressions which have been used have, many of them, histories of their own and we have taken them bodily from the phraseology of Constitutions of the West in many places. Therefore it could not be helped because of the limitation of those who were charged with drafting that the draft had to be prepared in English. I do not think we have lost anything by that but when once a particular article is finally adopted in this House in the English language, we shall see to it that as correct and perfect a translation is produced as possible and in the language which will be accepted by the Constituent Assembly as the language for our national purposes. So I would ask the Members not to anticipate the discussion which we shall have on the question of language. That will come a little later but I promise this that as soon as that question is settled, we shall have the translation revised or prepared in that particular language which is accepted and we shall put the translated Constitution also before the House for acceptance.

*[Mr. President, you had made a specific commitment that when the constitution would be placed before us, its original would be in our national language. I had also put a question to you at that time and in your reply also you did say that the original draft of the constitution to be placed before us would be in our language. But the draft Constitution placed before us by Dr. Ambedkaris in English. As the constitution now placed before us is in English I would like to know when the constitution originally drafted in our national language and about which you have given us an assurance will be brought before us.]

*[Mr. President, I would like to inquire whether after the adoption of the article relating to the national language, each clause would be taken up in the National Language for adoption just in the same manner as the clauses in the English Draft are taken up for final adoption after these have been duly amended.]

*[Every article will be taken up.]

Sir, I only want to make this suggestion that before taking up the Constitution clause by clause will it not be better if you very graciously permit us to take up the question of national language and have a decision about it. Because if we first take up the question of the national language and decide it, then once for all the hatchet is buried (Cheers). You can have the discussions of 10 or 15 clauses in English. The Committee will begetting the translations ready the next day and the whole translation of that part will be before the House which will be called upon to take it into consideration and then it shall be deemed to have been passed by the House. Therefore I suggest you may be pleased to permit this House to take up the question of the national language first before taking up the Constitution clause by clause. The question of national language comes in somewhere in clause 99 of the Constitution which may take long. This question bristles with many difficulties and some of us feel it to be fundamentally embedded with our future. There are other members who do not attach importance to it. Therefore I would request you to take up this question first and give us an opportunity to decide it and afterwards like the Constitution in English clause by clause and then give us opportunity to take them in Hindi as well.

May I state that the very reason which he has adduced for taking up the question of language in the beginning has induced me to put it off to a later stage. The reason which he has given is that there are differences of opinion, some people holding very strongly one view and others holding the other view equally strongly. I suggest that it is much better to discuss at any rate the fundamentals of the Constitution in a calm atmosphere before our tempers have got frayed. I therefore suggest that we should go on with the Constitution and discuss each item and when we have done that much–it will not in any way prejudice the question of language–the language question will be decided on its merits by the House and when that decision has been taken, every article will be passed ultimately in that language also. Therefore nothing is lost. Only, we do not lost temper to begin with.

*[Mr. President, Sir, the proposal that I want to place before you is this. On the first occasion when I delivered my speech in Hindi in this House, I had moved an amendment to the effect that the constitution should be framed in our national language and that the English version should be treated as its translation. Therefore I want to submit that when the discussion on the English version of the Constitution is over and it has been fully passed and when with your permission a decision has also been reached in regard to the national language, I shall place the proposal before you that the constitution in the national language should be considered as the original one. It will be insulting for us to adopt the translation of the English version. No nation has so far done so.

I admit that the Members would speak in English in this debate. I shall also speak in English and in fact want to do so but later I shall speak in Hindi. I wish to inform you that I want to place before you a motion when this discussion is over. It will be to the effect that the English version of the Constitution will be considered the translation of the constitution in the national language and the latter will be taken to be the original one. The English version will be styled as translation. I request that I maybe told as to when I may table that motion before you.]

*[This Assembly is entitled to say whether the constitution will be passed in Hindi or Urdu and that version will be taken to be the original one. The other versions will be considered as its translations. You have the power to do so.]

Sir, your orders came regarding the translations. Complete translations have been made in certain languages and I have no quarrel with that but in the process of Constitution making it is imperative that the people of our country – whatever may be their spoken language – they should understand it. So in your scheme of translation if you will kindly include, in addition to Hindi and Urdu, other major languages of India, it would be very convenient for everyone to understand and thereby, whatever may be the Rashtrabhasha afterwards, it will not be said that the proceedings were carried on in a language or languages which were not intelligible to all parts of the country. This is my suggestion. I have no disrespect for Hindi nor have I any attachment to English but as the Constitution is a very important thing. I think it should be made intelligible to all the people of the country. So my prayer is you might kindly include in your scheme of translation at least the major languages of India and I don’t think it will be difficult for you to arrange that.

Mr. President, you have made an announcement regarding the procedure you propose to follow in connection with the Bill before us, that will have a very important bearing on the discussions that will take place shortly. You have drawn our attention to two points.

The first point is that as the principles underlying this Bill were accepted by the Assembly a few months back, no amendment should be brought forward which would question any of these principles or would seek to make any alteration in them. Sir, this is a matter……

I qualified that by “ordinarily”.

It all depends on how the Chair will interpret this word. But I remember that when the discussions on the principles embodied in the Bill were going on, it was said several times that we should have a better opportunity for expressing our opinions later when the whole picture was before us. This is a matter that, I venture to think, Sir, deserves your serious attention. We might, a few months back, have accepted certain conclusions, but if, either after studying the Act as a whole, or after further reflection, any of us comes to the conclusion that any of these principles should be modified or completely altered, his right to express his opinion should not be questioned.

I may say at once that I do not propose to rule out any discussion. It will be for the House to decide whether it will go back on any of its decisions. As Chairman, I do not propose to rule out any discussion or reconsideration.

The House will certainly have the right to decide whether it will go back on any of its previous decisions. If it does not approve any change in the principles accepted by it some time ago, it will be open to it to throw out any suggestion for a change made by any Member. But what I have said, is due to the fact that I am under the impression that it was your intention to rule out certain amendments.

I am sorry if I left that impression.

I am very glad to hear from you, Sir, that this is not your intention. It is therefore not necessary for me to discuss this aspect of your pronouncement any more.

I now come to the second point which you asked the House to bear in mind in giving notice of amendments in future. You said that you would allow amendments to be proposed till 5 o’clock on Sunday next, but that thereafter you would not admit any new amendment for discussion, unless it seemed to you to relate to a matter of importance. I think, Sir, we all appreciate the substance of what you have said. As far as possible, our discussion should be canalized in proper channels and should relate to such points only a sought to be considered by the House again. Your advice therefore in regard to the character of the amendments would naturally carry great weight with every Member of this House. But I submit, Sir, that no amendment, no matter when received, ought to be automatically ruled out on the ground that it was not received by 5 o’clock on Sunday afternoon. It is the duty of the Chair to regulate the discussion and I have no doubt that every Member of this House is anxious to help the Chair in its onerous task, particularly as the Chair is occupied by a person of your eminence. But we have under the rules certain definite rights of which every Member of the House ought to be jealous. We have under the rules the right to give notice of amendments at any stage we like, and provided they are received within the time allotted by the rules, our right to put forward new amendments cannot be questioned. It cannot be questioned even by you, Sir.

I therefore suggest that when you consider any amendment that is proposed, to be superfluous, or to relate to a very unimportant matter, you may well advise the Member concerned to save the time of the House by withdrawing it. But should he insist on expression his view, even on an unimportant matter, I hope that you, whose duty it is to maintain our rights and privileges unimpaired, will not take away by executive discretion his right to propose his amendment. Sir, this is a matter of great importance. It relates to a question of principle. I do not think that in practice any conflict will arise between the Chair and any member of this House but I am anxious that no right, not even the least, that the rules enable us to enjoy should be taken away from us or whittled down either directly or indirectly. I hope that my observations will receive the attention of the Chair and that my remarks will be taken in the spirit in which they have been made. We all mean to be respectful to you. We listen to whatever you say with great attention and with a desire to act up to your advice but we do earnestly request you not to make any attempt to trench even on the smallest of our privileges. We ask you to standup for them should anybody attack them and I trust that the discussion will be carried on in such a way as to enable us to feel that you are the guardian of our dignity and privileges and will maintain unimpaired every right that the House enjoys at present under the rules.

I hope I have not given any cause so far in this Assembly to any Member to complain that I have acted in such a way as to take away any of his rights and I hope to continue the tradition in the future also.

Sir, I beg to draw your attention to the fact that I have already given notice of a motion to the effect:

“That the consideration of the Draft Constitution of India be postponed till the election of a fresh and competent Constituent Assembly on the basis of Joint Electorates and the formation of political rather than communal parties in India.“

I also beg to draw your attention to your ruling when I proposed an amendment to the same effect on the occasion of the presentation of the report on the principles of a Model provincial constitution, viz., that the consideration of the provincial constitution be postponed unless and until we have considered the Union Constitution…..

We shall take up your amendment in due course.

I want to place my motion first.

The motion that the Bill be considered has not been made and therefore the amendment cannot be moved at this stage.

That is what I am saying. We shall take it up in due course.

The Assembly then adjourned for Lunch till Three of the Clock.

The Assembly re-assembled after lunch at Three of the Clock, Mr. President (The Honourable Dr. Rajendra Prasad) in the Chair.

Mr. President, before we rose for lunch, the question put before you for your consideration was whether the procedure which you had announced regarding the discussions here held good or whether you will please accede to the request made by my friend Pandit Hirday Nath Kunzru. According to the rules we have the right to give two days’ notice of amendments if they are to be considered valid. I need not quote the relevant rule. It is known to everybody. We followed it last time. When the draft of the Constitution was sent to us, I and many others here thought naturally that the same old procedure with regard to discussion will be followed. Now, many of my friends may not have sent in their amendments in full in the hope that we would discuss these matters here and then give notice of our amendments after a discussion between ourselves. The old arrangement of two days’ notice enabled us to meet in groups or parties and discuss and send in amendments. If this practice is to be guillotined and we are not to be permitted to give notice of amendments as we proceed clause by clause, it will not be fair for those who have only just now joined the Assembly. There are many who have signed the Register today and got the papers of the Assembly a few hours ago. The draft Constitution is a huge volume which we want to read and consider. If you accede to the request of my friend Mr. Kunzru and permit the new-comers to study the Draft Constitution as the discussion proceeds it will facilitate them to send their amendments in time and have their say. Otherwise, the new arrivals will not be accommodated at all.

Mr. President, we are the Constituent Assembly and are making the Constitution. An ordinary law which is considered by the Legislative Assembly and passed can be amended once very month or so. But the Constitution is not amended every now and then. We are making a Constitution for centuries to come and it cannot be amended easily, as easily as we can amend a legislative enactment. Therefore, full facilities should be given to the Members of this House to have their say.

Therefore, I repeat the request that you may please consider that the two days’ time given in the rules is not taken away and allow amendments subject to their relevancy to the motion under consideration. Amendments may not be moved which have the effect of negativing the main motion except as permitted by the Chairman. Notice of amendments to a motion must be given one clear day before the motion is moved in the Assembly. This rule being there, I submit ,unless we change the rules…………..

The relevant rule is 38-0.

It says:

“If notice of a proposed amendment has not been given two clear days before the day no which the Constitution or the Bill, as the case may be, is to be considered, any member may object to the moving of the amendment, and such objection shall prevail, unless the President in his discretion allows the amendment to be moved.”

Do you mean to interpret this rule 38-0 in such a way that the whole Constitution………

I hope the Honourable Member will not drive me to give a decision on that point today. You had better leave it there. (Laughter).

Arising from the pronouncement made by you this morning, may I seek clarification on two points?

*[Mr. President, I find that Honourable Members stand up to intervene in the debate. I request that I may also be given a chance to speak.]

May I seek a little clarification of the announcement you made this morning? You were pleased to say that the Assembly would adjourn on 9th December for a few days. Do we adjourn on that day irrespective of whether we complete the consideration of the Constitution or not?

Nothing of the sort. I only suggested some sort of time table which I considered to be fair. It is for the House to decide whether they would go on up to 9th of December next year. (Laughter).

Are we going to have a recess from 9th December to a date to be specified later?

It all depends on the business on hand. I have suggested more than once that I do not want to curtail discussion. As we are considering the Constitution of the country, we shall not do anything in a hurry; but at the same time I do not want waste time.

Are we going to adjourn on the 9th December, irrespective of whether we complete the consideration of the Constitution or not?

That we shall see.

You were pleased to remark in the morning as regards the non-participation of Hyderabad and Bhopal, that it is a matter entirely for the Government to consider. Mr. President, according to our Rules you have power to call upon the rulers of Hyderabad and other States to send representatives to the Constituent Assembly. But, you were pleased to say that it is a matter in the hands of Government. I do not know how the Government comes into this affair. You are fully authorised to call upon the rulers to send their representatives to the Assembly.

Sitting in this Assembly, I have no right to compel anybody to do anything. Those who have come in are entitled to participate in the deliberations of this Assembly and those who have not come, we cannot force them to come. It is for the Government to deal with them.

*[Mr. President, as far as I remember you had announced in the last session that the Constitution to be presented here would be in Hindi and that it might be translated into English. But the statement you have made today has been a source of disappointment in as much as we learn that we have to discuss the very Draft that has been prepared by the Drafting Committee in English. We have before us its Hindi version also. I do not understand why we should not take into consideration the Hindi version of the Draft when it is before us. We may take up for consideration the Hindi version of the Draft clause by clause and if any portion is found to be translated in rather difficult language. Dr. Ambedkar who himself is a great scholar of the Sanskrit language, may explain such portion from the English Draft to those who are unable to follow the version in Hindi. It is necessary for every county to frame its constitution in its own language. We belong to a country that has its own language. We should therefore discuss it clause by clause in our own language. The Draft prepared in a foreign language should not be presented to this House for discussion.

Sir, perhaps you remember that at the commencement of the first session of the Constituent Assembly I made a request that the discussion in this House should be carried on in a language which is understood by the people of this country. We should not proceed in this House as if it were the British Parliament. The word `Dominion’ is entirely foreign in character. I remember a saying of the late Moulana Mohammad Ali. He used to say that the word` Dominion’ might be applicable to Africa, South Africa, New Zealand, Australia and Tasmania. These are the dominions where our alien rulers had founded colonies and established cantonments. But India cannot be said to be a cantonment for the British. They went to the countries I have already named and established there their colonies and cantonments; they also carried their language with them and the people of those countries are English speaking. But this cannot be said in our case. We have our own language, our own civilization which has come down to us through hundreds of centuries; so also we have our own literature. Just as the English people can take pride in their literature, in Shakespeare and Milton, we too can be proud of the works of our Kalidas, Tulsidas, Jayasi and Soordas. It will be matter of deep shame for a country which has developed a language of its own, to frame its first free Constitution in a foreign language. Therefore, I would like to entreat you, to pray to you that the Hindi version of the Draft Constitution should be placed before this House as the original Draft of the Constitution. The clauses of the Hindi version should be discussed here and the English Draft should not be presented here for discussion. It should be treated only as a translation.

The English have quit India. Their cantonments are no longer here. Following your example and the example of your colleagues and other respected leaders who have immortalized their names in our history by eliminating the English rule from our land and whose names have become memorable, we should remove the word `Dominion’ from the Draft and I am sure it will be removed. It will, I think be agitated in detail in this House and many Members would express themselves on it. But this is a matter for future discussion. Just now the question before us is whether we have any language of our own and a culture of our own; whether we have a language of our songs, of our poems and for the expression of our thoughts and emotions. We should frame our Constitution in the same language in which we would express our feelings. The Preamble of the Draft says: “We, the people of India . . . . . . . . . give to ourselves this Constitution.” Here the term “We the people of India” means not the few men who are sitting in this House but the dumb millions of India and on whose behalf we are functioning here. Therefore the Constitution that is being presented here must be in the language we understand. It is a matter of regret that many of our veteran leaders have begun to say that the problem of language has not yet been solved; that our language has not been reformed and that English has to stay. Such things are said sometimes. I do not want here to mention the names of those leaders. But since they say that we have no language of our own, I want to tell them that ours is a developed language, a rich language which is capable of expressing high thoughts and sentiments. It has a rich and a good vocabulary. We have inherited our language from our ancient sages, we have inherited it from Kautilya’s Artha Shastra, from our ancient literature which has such gems as the Mahabharat at and the Ramayana. We have developed our language taking words from these epics. Therefore it can not be said. . . .]

*[Excuse me, I do not understand what you are discussing. All the matters to which you are referring are those on which there is already considerable agreement.]

*[I am only submitting that the original draft of the Constitution which we are to discuss here should be in Hindi and not in English. Therefore we should have liberty to table amendments on the clauses of the Hindi version of the Draft treating it as the original one. I beg to propose this with the idea that it would indicate that we have our own language. We do not deem our land to be such a dominion within the British Empire as can express itself only in English.

I would like to say a few words more. Fortunately or unfortunately our brethren who live in those coastal regions where the English landed for the first time have acquired considerable proficiency in English. It is they who feel the greatest embarrassment when Hindi is mentioned as the national language. It had been the great good fortune of the people of Madras that their scholars gave to India a sublime message based on the Vedic literature and culture. Similarly it was their lot that the English…….

*[I would like to point out to you that you are continuing to talk on a subject on which there is no dispute. All admit that we can and will frame our constitution in our language. There is no scope for any further discussion on this matter. Previously also the question has been discussed many times and I am sure that at the appropriate occasion it will be adopted.]

*[I am talking at present, of tabling amendments in Hindi.]

*[You can table amendments in Hindi if you so desire. But how can an amendment in Hindi fit in the clause that is in English. There will be difficulty for me but, however, if you wish to table any amendment in Hindi you can do so.]

*[Mr. President, I want to invite your attention to the fact that while discussing the Report of the Minorities Board this House had decided on the last occasion that the consideration of the problem of Sikh rights should be held up as the conditions in the East Punjab were not normal. Today, we have got before us recommendations relating to all minorities but so far Sikhs are concerned, no decision has been taken as yet.]

*[When this question is taken up you will be free to say what you want to say about it.]

*[Sir, You have observed that amendments may be sent within two days but nothing has been decided regarding this question.]

*[You can send your amendments, after a decision has been taken in this matter.]

Mr. President, Sir, I do not wish to prolong the discussion on this subject. I simply wish to draw your attention to two important points. The rule as framed is all-comprehensive, the time of two days is given for giving amendments before the Constitution is taken up. Your discretion, Sir, is still left wide open, and I hope it will be used generously. I am saying this not that I am not convinced that it will be used generously but to assure my friends that, if there is anything material, they can rely on you that it will be given favourable consideration.

There is a second point on which I require your indulgence. Amendments to amendments can only come forward when the amendments are before the House. Therefore in that category you will have to relax your ruling and give us an opportunity to give amendments to amendments even after that time.

Certainly.

Thirdly, I wish to stress that this controversy about language may be happily solved if all those friends of ours who are interested in the Hindi version are formed into a Committee from the beginning to go forward with the work of translating or putting forward a Hindi version also. Amendments also may be sent in Hindi provided the office arranges to give us an English translation as well. So in this manner we will be able to achieve both the objectives. An amendment may be given in any language which is approved by the Constituent Assembly provided a translation appears on the Order Paper simultaneously.

Fourthly, I should like to invite the attention of the House to the fact that the Constitution is being made for – I would not say for generations – as long as it serves our purpose. The United States of America has made amendments to its constitution and about twenty amendments have already been made. There the process is so difficult. As you will remember, that not only has to be got through the two Houses, but it must be approved by each unit of the U.S.A. Our position is not so bad. But there is one thing, Sir, on which I would require your indulgence, and that is the question of the boundaries of existing or new provinces. That matter, Sir, after the constitution will become so difficult that I am sure it will become well nigh impossible to do anything towards this end. If it is the will of the House that the present boundaries should be changed in any manner, it would be meet and proper that before we finalise the Constitution in the next session after the recess, we should have a picture of the provinces as they will be constituted in the immediate future and not leave it for further action in a remote future.

I think that the suggestion is somewhat premature. We are awaiting the report of the Commission which we have appointed and we shall consider it at that stage.

Before finalising, we may be able to move amendments to those recommendations as and when it comes up. I simply invite the attention of the House to the urgency of the matter and to the matter being given full consideration and finalization.

*[Sir, I submit that the period of two hours that will be given to us tomorrow for general discussion is too short. It is a different matter that hundreds of amendments will be received. When every member gets an opportunity of expressing his views, the amendments that are tabled after a discussion of a few days, are altered. The amendments are not referred to in the discussion. Therefore I request that if we are given three or four days’ time for discussion and every Member is asked to observe the rule that he should not speak for more than fifteen minutes, every Member then will have the satisfaction that he has made his contribution in the House in the framing of the constitution. I submit that one day means only five hours time. If Dr. Ambedkar takes it up at four today and takes half the time tomorrow, there will hardly be left any time for us. Therefore I humbly request that we may be given an opportunity of speaking on this highly important constitution. The opportunity of framing the constitution does not come over and over again and everyone desires to speak out whatever he has to say for his country and nation. I want to submit also that whatever we speak here is not meant for this House only or for the present time only. Whatever is spoken here will be read even after hundred or two hundred or four hundred years and the people will come to know of the views of their ancestors one particular point. They will interpret it accordingly. Therefore, Sir, I think we the Members in this House will be highly obliged if at least four days are granted to us. Everyone of us wants only fifteen minutes and I want to tell you on behalf of other Members also that if this opportunity is given to us, we shall sit together and come to a decision regarding the hundreds of amendments that may be brought forward and the Members of this House will help you in finalising the constitution as quickly as possible.]

*[We shall consider this later on. The time now being spent on the preliminary discussion reduces the time available for detailed discussion. Therefore, I would ask that you allow the real work to start.]

*[Mr. President, at the very outset I would like to enquire whether the Honourable Dr. Ambedkar has given any notice of his intention to introduce the Draft Constitution as required by the Rule 38-L or not. I am asking for this information, because if no such notice has been given, I am afraid he can not move for consideration. According to the rules five days’ notice is necessary.]

*[Yes! It has been included there. It has been included in the Agenda. It being a re-draft all the amendments will be taken up again.]

*[Another point which I wanted to bring to your notice falls under Rules 38-M. The copy of the draft constitution, which is a re-draft, has been given to us just today at the time when you were adjourning the House for lunch, whereas it should have reached us much earlier. I think all the Members have not received a copy each so far. According to Rule 38-M such copies should reach the Members at least three days before, more particularly for the reason that it contains various reports on new matters. Unless it has been thoroughly read and studied, how can amendments be sent?]

*[Which copy are you referring to? The Draft Constitution placed before you by Dr. Ambedkar of 21st February, the copies of which were distributed, will be moved by him and the amendments on it will be proposed as amendments and they will be moved on behalf of the Drafting Committee.]

*[The third point for submission on which I respectfully want to lay more emphasis is regarding the interpretation of Rule 38-O. In my opinion the view that the words “two clear days before the ‘day’ on which the constitution is to be considered” in Rule 38-O is that all the amendments should reach the office by Sunday before 5 P.M., is not correct for the reason that the constitution shall not be taken up for consideration on the 9th November only; rather, its consideration will continue from day to day when the clauses will be discussed. There will be other dates further on after which it would be stated that the Constitution will be considered on those particular dates. That being the case, Members have the right to send in their amendments, two days before the date when the particular amendments shall be discussed.]

*[Let us not take a decision on this point at this stage.]

*[I am aware that you want to give full opportunity to the Members for discussion and that their right of giving notice of amendments should remain intact. Every Member has confidence in the matter of the exercise of your discretion. But in my humble opinion, the question of discretion does not arise here, because according to my interpretation, every Member can send in amendments as a matter of right. This is also the intention of Rules 38-P and 38-Q. Your order that Members should send their amendments by 5 o’clock on Sunday goes in a way, prima facie, against the Members, which is not in order and should be reviewed. You may not decide it now, if you do not want to, though incidentally and in a way, the decision is there. In my humble opinion, if without reviewing the order, you extend the date, instead of 7th, to 10th and decide the question, when occasion arises, then nobody will have any grievance.]

On a point of order, Mr. President, Sir, most of the honourable Members who spoke previously know the English language very well. We are very sorry to bring it to your notice that most of the Members, especially Members coming from Madras, from Bengal, Bombay, Assam and many other places cannot understand Hindi or Hindustani. We have to sit almost like dumb people. Mr. President, Sir, you are here to protect the interests of all the Members. I would,  therefore, request you to see that all those members who know English and who are able to speak in English are made to speak in English.

MOTION re. DRAFT CONSTITUTION

I think we shall now proceed with the discussion. I call upon the Honourable Dr. Ambedkar to move his motion.

Mr. President, Sir, I introduce the Draft Constitution as settled by the Drafting Committee and move that it be taken into consideration.

The Drafting Committee was appointed by a Resolution passed by the Constituent Assembly on August 29, 1947.

The Drafting Committee was in effect charged with the duty of preparing a Constitution in accordance with the decisions of the Constituent Assembly on the reports made by the various Committees appointed by it such as the Union Powers Committee, the Union Constitution Committee, the Provincial Constitution Committee and the Advisory Committee on Fundamental Rights, Minorities, Tribal Areas, etc. The Constituent Assembly had also directed that in certain matters the provisions contained in the Government of India Act, 1935, should be followed. Except on points which are referred to in my letter of the 21st February 1948 in which I have referred to the departures made and alternatives suggested by the Drafting Committee, I hope the Drafting Committee will be found to have faithfully carried out the directions given to it.

The Draft Constitution as it has emerged from the Drafting Committee is a formidable document. It contains 315 Articles and 8 Schedules. It must be admitted that the Constitution of no country could be found to be so bulky as the Draft Constitution. It would be difficult for those who have not been through it to realize its salient and special features.

The Draft Constitution has been before the public for eight months. During this long time friends, critics and adversaries have had more than sufficient time to express their reactions to the provisions contained in it. I dare say that some of them are based on misunderstanding and inadequate understanding of the Articles. But there the criticisms are and they have to be answered.

For both these reasons it is necessary that on a motion for consideration I should draw your attention to the special features of the Constitution and also meet the criticism that has been levelled against it.

Before I proceed to do so I would like to place on the table of the House Reports of three Committees appointed by the Constituent Assembly (1) Report of the Committee on Chief Commissioners’ Provinces (2) Report of the Expert Committee on Financial Relations between the Union and the States, and (3) Report of the Advisory Committee on Tribal Areas, which came too late to be considered by that Assembly though copies of them have been circulated to Members of the Assembly. As these reports and the recommendations made therein have been considered by the Drafting Committee it is only proper that the House should formally be placed in possession of them.

Turning to the main question. A student of Constitutional Law if a copy of a Constitution is placed in his hands is sure to ask two questions. Firstly what is the form of Government that is envisaged in the Constitution; and secondly what in the form of the Constitution? For these are the two crucial matters which every Constitution has to deal with. I will begin with the first of the two questions.

In the Draft Constitution there is placed at the head of the Indian Union a functionary who is called the President of the Union. The title of this functionary reminds one of the President of the United States. But beyond identity of names there is nothing in common between the forms of Government prevalent in America and the form of Government proposed under the Draft Constitution. The American form of Government is called the Presidential system of Government. What the Draft Constitution proposes is the Parliamentary system. The two are fundamentally different.

Under the Presidential system of America, the President is the Chief head of the Executive. The administration is vested in him. Under the Draft Constitution the President occupies the same position as the King under the English Constitution. He is the head of the State but not of the Executive. He represents the Nation but does not rule the Nation. He is the symbol of the nation. His place in the administration is that of a ceremonial device on a seal by which the nation’s decisions are made known. Under the American Constitution the President has under him Secretaries in charge of different Departments. In like manner the President of the Indian Union will have under him Ministers in charge of different Departments of administration. Here again there is a fundamental difference between the two. The President of the United States is not bound to accept any advice tendered to him by any of his Secretaries. The President of the Indian Union will be generally bound by the advice of his Ministers. He can do nothing contrary to their advice nor can he do any thing without their advice. The President of the United States can dismiss any Secretary at any time. The President of the Indian Union has no power to do so long as his Ministers command a majority in Parliament.

The Presidential system of America is based upon the separation of the Executive and the Legislature. So that the President and his Secretaries cannot be members of the Congress. The Draft Constitution does not recognise this doctrine. The Ministers under the Indian Union are members of Parliament. Only members of Parliament can become Ministers. Ministers have the same rights as other members of Parliament, namely, that they can sit in Parliament, take part in debates and vote in its proceedings. Both systems of Government are of course democratic and the choice between the two is not very easy. A democratic executive must satisfy two conditions – (1) It must be a stable executive and (2) it must be a responsible executive. Unfortunately it has not been possible so far to devise a system which can ensure both in equal degree. You can have a system which can give you more stability but less responsibility or you can have a system which gives you more responsibility but less stability. The American and the Swiss systems give more stability but less responsibility. The British system on the other hand gives you more responsibility but less stability. The reason for this is obvious. The American Executive is a non-Parliamentary Executive which means that it is not dependent for its existence upon a majority in the Congress, while the British system is a Parliamentary Executive which means that it is not dependent for its existence upon a majority in the Congress, while the British system is a Parliamentary Executive which means that it is dependent upon a majority in Parliament. Being a non-Parliamentary Executive, the Congress of the United States cannot dismiss the Executive. A Parliamentary Government must resign the moment it loses the confidence of a majority of the members of Parliament. Looking at it from the point of view of responsibility, a non-Parliamentary Executive being independent of Parliament tends to be less responsible to the Legislature, while a Parliamentary Executive being more dependent upon a majority in Parliament become more responsible. The Parliamentary system differs from a non-Parliamentary system in as much as the former is more responsible than the latter but they also differ as to the time and agency for assessment of their responsibility. Under the non-Parliamentary system, such as the one that exists in the U.S.A., the assessment of the responsibility of the Executive is periodic. It takes place once in two years. It is done by the Electorate. In England, where the Parliamentary system prevails, the assessment of responsibility of the Executive is both daily and periodic. The daily assessment is done by members of Parliament, through questions, Resolutions, No-confidence motions, Adjournment motions and Debates on Addresses. Periodic assessment is done by the Electorate at the time of the election which may take place every five years or earlier. The Daily assessment of responsibility which is not available under the American system it is felt far  more effective than the periodic assessment and far more necessary in a country like India. The Draft Constitution in recommending the Parliamentary system of Executive has preferred more responsibility to more stability.

So far I have explained the form of Government under the Draft Constitution. I will now turn to the other question, namely, the form of the Constitution.

Two principal forms of the Constitution are known to history – one is called Unitary and the other Federal. The two essential characteristics of a Unitary Constitution are:(1) the supremacy of the Central Polity and (2) the absence of subsidiary Sovereign polities. Contrariwise, a Federal Constitution is marked: (1) by the existence of a Central polity and subsidiary polities side by side, and (2) by each being sovereign in the field assigned to it. In other words. Federation means the establishment of a Dual Polity. The Draft Constitution is, Federal Constitution inasmuch as it establishes what may be called a Dual Polity. This Dual Polity under the proposed Constitution will consist of the Union at the Centre and the States at the periphery each endowed with sovereign powers to be exercised in the field assigned to them respectively by the Constitution. This dual polity resembles the American Constitution. The American polity is also a dual polity, one of it is known as the Federal Government and the other States which correspond respectively to the Union Government and the States Government of the Draft Constitution. Under the American Constitution the Federal Government is not a mere league of the States nor are the States administrative units or agencies of the Federal Government. In the same way the Indian Constitution proposed in the Draft Constitution is not a league of States nor are the States administrative units or agencies of the Union Government. Here, however, the similarities between the Indian and the American Constitution come to an end. The differences that distinguish them are more fundamental and glaring than the similarities between the two.

The points of difference between the American Federation and the Indian Federation are mainly two. In the U.S.A. this dual polity is followed by a dual citizenship. In the U.S.A. there is a citizenship of the U.S.A. But there is also a citizenship of the State. No doubt the rigours of this double citizenship are much assuaged by the fourteenth amendment to the Constitution of the United States which prohibits the States from taking away the rights, privileges and immunities of the citizen of the United States. At the same time, as pointed out by Mr. William Anderson, in certain political matters, including the right to vote and to hold public office, States may and do discriminate in favour of their own citizens. This favoritism goes even farther in many cases. Thus to obtain employment in the service of a State or local Government one is in most places required to the be a local resident or citizen. Similarly in the licensing of persons for the practice of such public professions as law and medicine, residence or citizenship in the State is frequently required; and in business where public regulation must necessarily be strict, as in the sale of liquor, and of stocks and bonds, similar requirements have been upheld.

Each State has also certain rights in its own domain that it holds for the special advantage of its own citizens. Thus wild game and fish in a sense belong to the State. It is customary for the States to charge higher hunting and fishing license fees to non-residents than to its own citizens. The States also charge non-residents higher tuition in State Colleges and Universities, and permit only residents to be admitted to their hospitals and asylums except in emergencies.

In short, there are a number of rights that a State can grant to its own citizens or residents that it may and does legally deny to non-residents, or grant to non-residents only on more difficult terms than those imposed on residents. These advantages, given to the citizen in his own State, constitute the special rights of State citizenship. Taken all together, they amount to a considerable difference in rights between citizens and non-citizens of the State. The transient and the temporary sojourner is everywhere under some special handicaps.

The proposed Indian Constitution is a dual polity  with a single citizenship. There is only one citizenship for the whole of India. It is Indian citizenship. There is no State citizenship. Every Indian has the same rights of citizenship, no matter in what State he resides.

The dual polity of the proposed Indian Constitution differs from the dual polity of the U.S.A. in another respect. In the U.S.A. the Constitutions of the Federal and the States Governments are loosely connected. In describing the relationship between the Federal and State Government in the U.S.A., Bryce has said:

“The Central or national Government and the State Governments may be compared to a large building and a set of smaller buildings standing on the same ground, yet distinct from each other.“

Distinct they are, but how distinct are the State Governments in the U.S.A. from the Federal Government? Some idea of this distinctness may be obtained from the following facts:

1. Subject to the maintenance of the republican form of Government, each State in America is free to make its own Constitution.    

2. The people of a State retain for ever in their hands, altogether independent of the National Government, the power of altering their Constitution.

To put it again in the words of Bryce:

“A State (in America) exists as a commonwealth by virtue of its own Constitution, and all State Authorities, legislative, executive and judicial are the creatures of, and subject to the Constitution.“

This is not true of the proposed Indian Constitution. No States (at any rate those in Part I) have a right to frame its own Constitution. The Constitution of the Union and of the States is a single frame from which neither can get out and within which they must work.

So far I have drawn attention to the difference between the American Federation and the proposed Indian Federation. But there are some other special features of the proposed Indian Federation which mark it off not only from the American Federation but from all other Federations. All federal systems including the American are placed in a tight mould of federalism. No matter what the circumstances, it cannot change its form and shape. It can never be unitary. On the other hand the Draft Constitution can be both unitary as well as federal according to the requirements of time and circumstances. In normal times, it is framed to work as a federal system. But in times of war it is so designed as to make it work as though it was a unitary system. Once the President issues a Proclamation which he is authorised to do under the Provisions of Article 275, the whole scene can become transformed and the State becomes a unitary state. The Union under the Proclamation can claim if it wants (1) the power to legislate upon any subject even though it may be in the State list, (2) the power to give directions to the States as to how they should exercise their executive authority in matters which are within their charge, (3) the power to vest authority for any purpose in any officer, and (4) the power to suspend the financial provisions of the Constitution. Such a power of converting itself into a unitary State no federation possesses. This is one point of difference between the Federation proposed in the Draft Constitution, and all other Federations we know of.

This is not the only difference between the proposed Indian Federation and other federations. Federalism is described as a weak if not an effete form of Government. There are two weaknesses from which Federation is alleged to suffer. One is rigidity and the other is legalism. That these faults are inherent in Federalism, there can be no dispute. A Federal Constitution cannot but be a written Constitution and a written Constitution must necessarily be a rigid Constitution. A Federal Constitution means division of Sovereignty by no less a sanction than that of the law of the Constitution between the Federal Government and the States, with two necessary consequences (1) that any invasion by the Federal Government in the field assigned to the States and vice versa is a breach of the Constitution and (2) such breach is a justiciable matter to be determined by the Judiciary only. This being the nature of federalism, a federal Constitution have been found in a pronounced form in the Constitution of the United States of America.

Countries which have adopted Federalism at a later date have attempted to reduce the disadvantages following from the rigidity and legalism which are inherent therein. The example of Australia may well be referred to in this matter. The Australian Constitution has adopted the following means to make its federation less rigid: (1) By conferring upon the Parliament of the Commonwealth large powers of concurrent Legislation and few powers of exclusive Legislation.(2) By making some of the Articles of the Constitution of a temporary duration to remain in force only “until Parliament otherwise provides.”

It is obvious that under the Australian Constitution, the Australian Parliament can do many things, which are not within the competence of the American Congress and for doing which the American Government will have to resort to the Supreme Court and depend upon its ability, ingenuity and willingness to invent a doctrine to justify it the exercise of authority.

In assuaging the rigour of rigidity and legalism the Draft Constitution follows the Australian plan on a far more extensive scale than has been done in Australia. Like the Australian Constitution, it has a long list of subjects for concurrent powers of legislation. Under the Australian Constitution, concurrent subjects are 39. Under the Draft Constitution they are 37. Following the Australian Constitution there are as many as six Articles in the Draft Constitution, where the provisions are of a temporary duration and which could be replaced by Parliament at anytime by provisions suitable for the occasion. The biggest advance made by the Draft Constitution over the Australian Constitution is in the matter of exclusive powers of legislation vested in Parliament. While the exclusive authority of the Australian Parliament to legislate extends only to about 3 matters, the authority of the Indian Parliament as proposed in the Draft Constitution will extend to 91 matters. In this way the Draft Constitution has secured the greatest possible elasticity in its federalism which is supposed to be rigid by nature.

It is not enough to say that the Draft Constitution follows the Australian Constitution or follows it on a more extensive scale. What is to be noted is that it has added new ways of overcoming the rigidity and legalism inherent in federalism which are special to it and which are not to be found elsewhere.

First is the power given to Parliament to legislate on exclusively provincial subjects in normal times. I refer to Articles 226, 227 and 229. Under Article 226 Parliament can legislate when a subject becomes a matter of national concern as distinguished from purely Provincial concern, though the subject is in the State list, provided are solution is passed by the Upper Chamber by 2/3rd majority in favour of such exercise of the power by the Centre. Article 227 gives the similar power to Parliament in a national emergency. Under Article 229 Parliament can exercise the same power if Provinces consent to such exercise. Though the last provision also exists in the Australian Constitution the first two are a special feature of the Draft Constitution.

The second means adopted to avoid rigidity and legalism is the provision for facility with which the Constitution could be amended. The provisions of the Constitution relating to the amendment of the Constitution divide the Articles of the Constitution into two groups. In the one group are placed Articles relating to (a) the distribution of legislative powers between the Centre and the States, (b) the representation of the States in Parliament, and (c) the powers of the Courts. All other Articles are placed in another group. Articles placed in the second group cover a very large part of the Constitution and can be amended by Parliament by a double majority, namely, a majority of not less than two thirds of the members of each House present and voting and by a majority of the total membership of each House. The amendment of these Articles does not require ratification by the States. It is only in those Articles which are placed in group one that an additional safeguard of ratification by the States is introduced.

One can therefore safely say that the Indian Federation will not suffer from the faults of rigidity or legalism. Its distinguishing feature is that it is a flexible federation.

There is another special feature of the proposed Indian Federation which distinguishes it from other federations. A Federation being a dual polity based on divided authority with separate legislative, executive and judicial powers for each of the two polities is bound to produce diversity in laws, in administration and in judicial protection. Upto a certain point this diversity does not matter. It may be welcomed as being an attempt to accommodate the powers of Government to local needs and local circumstances. But this very diversity when it goes beyond a certain point is capable of producing chaos and has produced chaos in many federal States. One has only to imagine twenty different laws-if we have twenty States in the Union-of marriage, of divorce, of inheritance of property, family relations, contracts, torts, crimes, weights and measures, of bills and cheques , banking and commerce, of procedures for obtaining justice and in the standards and methods of administration. Such a state of affairs not only weakens the State but becomes intolerant to the citizen who moves from State to State only to find that what is lawful in one State is not lawful in another. The Draft Constitution has sought to forge means and methods whereby India will have Federation and at the same time will have uniformity in all basic matters which are essential to maintain the unity of the country. The means adopted by the Draft Constitution are three:

(1) a single judiciary,    

(2) uniformity-in fundamental laws, civil and criminal, and    

(3) a common All-India Civil Service to man important posts.

A dual judiciary, a duality of legal codes and a duality of civil services, as I said, are the logical consequences of a dual polity which is inherent in a federation. In the U. S. A. the Federal Judiciary and the State Judiciary are separate and independent of each other. The Indian Federation though a Dual Polity has no Dual Judiciary at all. The High Courts and the Supreme Court form one single integrated Judiciary having jurisdiction and providing remedies in all cases arising under the constitutional law, the civil law or the criminal law. This is done to eliminate all diversity in all remedial procedure. Canada is the only country which furnishes a close parallel. The Australian system is only an approximation.

Care is taken to eliminate all diversity from laws which are at the basis of civic and corporate life. The great Codes of Civil & Criminal Laws, such as the Civil Procedure Code, Penal Code, the Criminal Procedure Code, the Evidence Act, Transfer of Property Act, Laws of Marriage Divorce, and Inheritance, are either placed in the Concurrent List so that the necessary uniformity can always be preserved without impairing the federal system.

The dual polity which is inherent in a federal system as I said is followed in all federations by a dual service. In all Federations there is a Federal Civil Service and a State Civil Service. The Indian Federation though a Dual Polity will have a Dual Service but with one exception. It is recognized that in every country there are certain posts in its administrative set up which might be called strategic from the point of view of maintaining the standard of administration. It may not be easy to spot such posts in a large and complicated machinery of administration. But there can be no doubt that the standard of administration depends upon the calibre of the Civil Servants who are appointed to these strategic posts. Fortunately for us we have inherited from the past system of administration which is common to the whole of the country and we know what are these strategic posts. The Constitution provides that without depriving the States of their right to form their own Civil Services there shall be an All India service recruited on an All- India basis with common qualifications, with uniform scale of pay and the members of which alone could be appointed to these strategic posts throughout the Union.

Such are the special features of the proposed Federation. I will now turn to what the critics have had to say about it.

It is said that there is nothing new in the Draft Constitution, that about half of it has been copied from the Government of India Act of 1935 and that the rest of it has been borrowed from the Constitutions of other countries. Very little of it can claim originality.

One likes to ask whether there can be anything new in a Constitution framed at this hour in the history of the world. More than hundred years have rolled over when the first written Constitution was drafted. It has been followed by many countries reducing their Constitutions to writing. What the scope of a Constitution should be has long been settled. Similarly what are the fundamentals of a Constitution are recognized all over the world. Given these facts, all Constitutions in their main provisions must look similar. The only new things, if there can be any, in a Constitution framed so late in the day are the variations made to remove the faults and to accommodate it to the needs of the country. The charge of producing a blind copy of the Constitutions of other countries is based, I am sure, on an inadequate study of the Constitution. I have shown what is new in the Draft Constitution and I am sure that those who have studied other Constitutions and who are prepared to consider the matter dispassionately will agree that the Drafting Committee in performing its duty has not been guilty of such blind and slavish imitation as it is represented to be.

As to the accusation that the Draft Constitution has produced a good part of the provisions of the Government of India Act, 1935, I make no apologies. There is nothing to be ashamed of in borrowing. It involves no plagiarism. Nobody holds any patent rights in the fundamental ideas of a Constitution. What I am sorry about is that the provisions taken from the Government of India Act, 1935, relate mostly to the details of administration. I agree that administrative details should have no place in the Constitution. I wish very much that the Drafting Committee could see its way to avoid their inclusion in the Constitution. But this is to be said on the necessity which justifies their inclusion. Grote. the historian of Greece, has said that:

“The diffusion of constitutional morality, not merely among the majority of any community but throughout the whole, is the indispensable condition of a government at once free and peaceable; since even any powerful and obstinate minority may render the working of a free institution impracticable, without being strong enough to conquer ascendency for themselves.“

By constitutional morality Grote meant “a paramount reverence for the forms of the Constitution, enforcing obedience to authority acting under and within these forms yet combined with the habit of open speech, of action subject only to definite legal control, and unrestrained censure of those very authorities as to all their public acts combined too with a perfect confidence in the bosom of every citizen amidst the bitterness of party contest that the forms of the Constitution will not be less sacred in the eyes of his opponents than in his own.” (Hear, hear.)

While everybody recognizes the necessity of the diffusion of Constitutional morality for the peaceful working of a democratic Constitution, there are two things interconnected with it which are not, unfortunately, generally recognized. One is that the form of administration has a close connection with the form of the Constitution. The form of the administration must be appropriate to and in the same sense as the form of the Constitution. The other is that it is perfectly possible to pervert the Constitution, without changing its form by merely changing the form of the administration and to make it inconsistent and opposed to the spirit of the Constitution. It follows that it is only where people are saturated with Constitutional morality such as the one described by Grote the historian that one can take the risk of omitting from the Constitution details of administration and leaving it for the Legislature to prescribe them. The question is, can we presume such a diffusion of Constitutional morality? Constitutional morality is not a natural sentiment. It has to be cultivated. We must realize that our people have yet to learn it. Democracy in India is only a top-dressing on an Indian soil, which is essentially undemocratic.

In these circumstances it is wiser not to trust the Legislature to prescribe forms of administration. This is the justification for incorporating them in the Constitution.

Another criticism against the Draft Constitution is that no part of it represents the ancient polity of India. It is said that the new Constitution should have been drafted on the ancient Hindu model of a State and that instead of incorporating Western theories the new Constitution should have been raised and built upon village Panchayats and District Panchayats. There are others who have taken a more extreme view. They do not want any Central or Provincial Governments. They just want India to contain so many village Governments. The love of the intellectual Indians for the village community is of course infinite if not pathetic (laughter). It is largely due to the fulsome praise bestowed upon it by Metcalfe who described them as little republics having nearly everything that they want within themselves, and almost independent of any foreign relations. The existence of these village communities each one forming a separate little State in itself has according to Metcalfe contributed more than any other cause to the preservation of the people of India, through all the revolutions and changes which they have suffered, and is in a high degree conducive to their happiness and to the enjoyment of a great portion of the freedom and independence. No doubt the village communities have lasted where nothing else lasts. But those who take pride in the village communities do not care to consider what little part they have played in the affairs and the destiny of the country; and why? Their part in the destiny of the country has been well described by Metcalfe himself who says:

“Dynasty after dynasty tumbles down. Revolution succeeds to revolution. Hindoo, Pathan, Mogul, Maratha, Sikh, English are all masters in turn but the village communities remain the same. In times of trouble they arm and fortify themselves. A hostile army passes through the country. The village communities collect their little cattle within their walls, and let the enemy pass unprovoked.“

Such is the part the village communities have played in the history of their country. Knowing this, what pride can one feel in them? That they have survived through all viscisitudes may be a fact. But mere survival has no value. The question is on what plane they have survived. Surely on a low, on a selfish level. I hold that these village republics have been the ruination of India. I am therefore surprised that those who condemn Provincialism and communalism should come forward as champions of the village. What is the village but a sink of localism, a den of ignorance, narrow-mindedness and communalism? I am glad that the Draft Constitution has discarded the village and adopted the individual as its unit.

The Draft Constitution is also criticised because of the safeguards it provides for minorities. In this, the Drafting Committee has no responsibility. It follows the decisions of the Constituent Assembly. Speaking for myself, I have no doubt that the Constituent Assembly has done wisely in providing such safeguards for minorities as it has done. In this country both the minorities and the majorities have followed a wrong path. It is wrong for the majority to deny the existence of minorities. It is equally wrong for the minorities to perpetuate themselves. A solution must be found which will serve a double purpose. It must recognize the existence of the minorities to start with. It must also be such that it will enable majorities and minorities to merge someday into one. The solution proposed by the Constituent Assembly is to be welcomed because it is a solution which serves this twofold purpose. To diehards who have developed a kind of fanaticism against minority protection I would like to say two things. One is that minorities are an explosive force which, if it erupts, can blow up the whole fabric of the State. The history of Europe bears ample and appalling testimony to this fact. The other is that the minorities in India have agreed to place their existence in the hands of the majority. In the history of negotiations for preventing the partition of Ireland, Redmond said to Carson “ask for any safeguard you like for the Protestant minority but let us have a United Ireland.“Carson’s reply was “Damn your safeguards, we don’t want to be ruled by you.” No minority in India has taken this stand. They have loyally accepted the rule of the majority which is basically a communal majority and not a political majority. It is for the majority to realize its duty not to discriminate against minorities. Whether the minorities will continue or will vanish must depend upon this habit of the majority. The moment the majority loses the habit of discriminating against the minority, the minorities can have no ground to exist. They will vanish.

The most criticized part of the Draft Constitution is that which relates to Fundamental Rights. It is said that Article 13 which defines fundamental rights is riddled with so many exceptions that the exceptions have eaten up the rights altogether. It is condemned as a kind of deception. In the opinion of the critics fundamental rights are not fundamental rights unless they are also absolute rights. The critics rely on the Constitution of the United States and to the Bill of Rights embodied in the first ten Amendments to that Constitution in support of their contention. It is said that the fundamental rights in the American Bill of Rights are real because they are not subjected to limitations or exceptions.

I am sorry to say that the whole of the criticism about fundamental rights is based upon a misconception. In the first place, the criticism in so far as it seeks to distinguish fundamental rights from non-fundamental rights is not sound. It is incorrect to say that fundamental rights are absolute while non-fundamental rights are not absolute. The real distinction between the two is that non-fundamental rights are created by agreement between parties while fundamental rights are the gift of the law. Because fundamental rights are the gift of the State it does not follow that the State cannot qualify them.

In the second place, it is wrong to say that fundamental rights in America are absolute. The difference between the position under the American Constitution and the Draft Constitution is one of form and not of substance. That the fundamental rights in America are not absolute rights is beyond dispute. In support of every exception to the fundamental rights set out in the Draft Constitution one can refer to at least one judgment of the United States Supreme Court. It would be sufficient to quote one such judgment of the Supreme Court in justification of the limitation on the right of free speech contained in Article 13 of the Draft Constitution. In Gitlow Vs. New York in which the issue was the constitutionality of a New York “criminal anarchy” law which purported to punish utterances calculated to bring about violent change, the Supreme Court said:

“It is a fundamental principle, long established, that the freedom of speech and of the press, which is secured by the Constitution, does not confer an absolute right to speak or publish, without responsibility, whatever one may choose, or an unrestricted and unbridled license that gives immunity for every possible use of language and prevents the punishment of those who abuse this freedom.“

It is therefore wrong to say that the fundamental rights in America are absolute, while those in the Draft Constitution are not.

It is argued that if any fundamental rights require qualification, it is for the Constitution itself to qualify them as is done in the Constitution of the United States and where it does not do so it should be left to be determined by the Judiciary upon a consideration of all the relevant considerations. All this, I am sorry to say, is a complete misrepresentation if not a misunderstanding of the American Constitution. The American Constitution does nothing of the kind. Except in one matter, namely, the right of assembly, the American Constitution does not itself impose any limitations upon the fundamental rights guaranteed to the American citizens. Nor is it correct to say that the American Constitution leaves it to the judiciary to impose limitations on fundamental rights. The right to impose limitations belongs to the Congress. The real position is different from what is assumed by the critics. In America, the fundamental rights as enacted by the Constitution were no doubt absolute. Congress, however, soon found that it was absolutely essential to qualify these fundamental rights by limitations. When the question arose as to the constitutionality of these limitations before the Supreme Court, it was contended that the Constitution gave no power to the United States Congress to impose such limitation, the Supreme Court invented the doctrine of police power and refuted the advocates of absolute fundamental rights by the argument that every state has inherent in it police power which is not required to be conferred on it expressly by the Constitution. To use the language of the Supreme Court in the case I have already referred to, it said:

“That a State in the exercise of its police power may punish those who abuse this freedom by utterances inimical to the public welfare, tending to corrupt public morals, incite to crime or disturb the public peace, is not open to question. . . . . “

What the Draft Constitution has done is that instead of formulating fundamental rights in absolute terms and depending upon our Supreme Court to come to the rescue of Parliament by inventing the doctrine of police power, it permits the State directly to impose limitations upon the fundamental rights. There is really no difference in the result. What one does directly the other does indirectly. In both cases, the fundamental rights are not absolute.

In the Draft Constitution the Fundamental Rights are followed by what are called “Directive Principles”. It is a novel feature in a Constitution framed for Parliamentary Democracy. The only other constitution framed for Parliamentary Democracy which embodies such principles is that of the Irish Free State. These Directive Principles have also come up for criticism. It is said that they are only pious declarations. They have no binding force. This criticism is of course superfluous. The Constitution itself says so in so many words.

If it is said that the Directive Principle have no legal force behind them, I am prepared to admit it. But I am not prepared to admit that they have no sort of binding force at all. Nor am I prepared to concede that they are useless because they have no binding force in law.

The Directive Principles are like the Instrument of Instructions which were issued to the Governor-General and to the Governors of the Colonies and to those of India by the British Government under the 1935 Act. Under the Draft Constitution it is proposed to issue such instruments to the President and to the Governors. The texts of these Instruments of Instructions will be found in Schedule IV of the Constitution. What are called Directive Principles is merely another name for Instrument of Instructions. The only difference is that they are instructions to the Legislature and the Executive. Such a thing is to my mind to be welcomed. Wherever there is a grant of power in general terms for peace, order and good government, it is necessary that it should be accompanied by instructions regulating its exercise.

The inclusion of such instructions in a Constitution such as is proposed in the Draft becomes justifiable for another reason. The Draft Constitution as framed only provides a machinery for the government of the country. It is not a contrivance to install any particular party in power as has been done in some countries. Who should be in power is left to be determined by the people, as it must be, if the system is to satisfy the tests of democracy. But whoever captures power will not be free to do what he likes with it. In the exercise of it, he will have to respect these instruments of instructions which are called Directive Principles. He cannot ignore them. He may not have to answer for their breach in a Court of Law. But he will certainly have to answer for them before the electorate at election time. What great value these directive principles possess will be realized better when the forces of right contrive to capture power.

That it has no binding force is no argument against their inclusion in the Constitution. There may be a difference of opinion as to the exact place they should be given in the Constitution. I agree that it is somewhat odd that provisions which do not carry positive obligations should be placed in the midst of provisions which do carry positive obligations. In my judgment their proper place is in Schedules III A& IV which contain Instrument of Instructions to the President and the Governors. For, as I have said, they are really Instruments of Instructions to the Executive and the Legislatures as to how they should exercise their powers. But that is only a matter of arrangement.

Some critics have said that the Centre is too strong. Others have said that it must be made stronger. The Draft Constitution has struck a balance. However much you may deny powers to the Centre, it is difficult to prevent the Centre from becoming strong. Conditions in modern world are such that centralization of powers is inevitable. One has only to consider the growth of the Federal Government in the U.S.A. which, notwithstanding the very limited powers given to it by the Constitution, has out-grown its former self and has overshadowed and eclipsed the State Governments. This is due to modern conditions. The same conditions are sure to operate on the Government of India and nothing that one can do will help to prevent it from being strong. On the other hand, we must resist the tendency to make it stronger. It cannot chew more than it can digest. Its strength must be commensurate with its weight. It would be a folly to make it so strong that it may fall by its own weight.

The Draft Constitution is criticized for having one sort of constitutional relations between the Centre and the Provinces and another sort of constitutional relations between the Centre and the Indian States. The Indian States are not bound to accept the whole list of subjects included in the Union List but only those which come under Defence, Foreign Affairs and Communications. They are not bound to accept subjects included in the Concurrent List. They are not bound to accept the State List contained in the Draft Constitution. They are free to create their own Constituent Assemblies and to frame their own constitutions. All this, of course, is very unfortunate and, I submit quite indefensible. This disparity may even prove dangerous to the efficiency of the State. So long as the disparity exists, the Centre’s authority over all-India matters may lose its efficacy. For, power is no power if it cannot be exercised in all cases and in all places. In a situation such as maybe created by war, such limitations on the exercise of vital powers in some areas may bring the whole life of the State in complete jeopardy. What is worse is that the Indian States under the Draft Constitution are permitted to maintain their own armies. I regard this as a most retrograde and harmful provision which may lead to the break-up of the unity of India and the overthrow of the Central Government. The Drafting Committee, if I am not misrepresenting its mind, was not at all happy over this matter. They wished very much that there was uniformity between the Provinces and the Indian States in their constitutional relationship with the Centre. Unfortunately, they could do nothing to improve matters. They were bound by the decisions of the Constituent Assembly, and the Constituent Assembly in its turn was bound by the agreement arrived at between the two negotiating Committees.

But we may take courage from what happened in Germany. The German Empire as founded by Bismark in 1870 was a composite State, consisting of 25 units. Of these 25 units, 22 were monarchical States and 3 were republican city States. This distinction, as we all know, disappeared in the course of time and Germany became one land with one people living under one Constitution. The process of the amalgamation of the Indian States is going to be much quicker than it has been in Germany. On the 15th August 1947 we had 600 Indian States in existence. Today by the integration of the Indian States with Indian Provinces or merger among themselves or by the Centre having taken them as Centrally Administered Areas there have remained some 20/30 States as viable States. This is a very rapid process and progress. I appeal to those States that remain to fall in line with the Indian Provinces and to become full units of the Indian Union on the same terms as the Indian Provinces. They will thereby give the Indian Union the strength it needs. They will save themselves the bother of starting their own Constituent Assemblies and drafting their own separate Constitution and they will lose nothing that is of value to them. I feel hopeful that my appeal will not go in vain and that before the Constitution is passed, we will be able to wipe off the differences between the Provinces and the Indian States.

Some critics have taken objection to the description of India in Article 1 of the Draft Constitution as a Union of States. It is said that the correct phraseology should be a Federation of States. It is true that South Africa which is a unitary State is described as a Union. But Canada which is a Federation is also called a Union. Thus the description of India as a Union, though its constitution is Federal, does no violence to usage. But what is important is that the use of the word Union is deliberate. I do not know why the word ‘Union’ was used in the Canadian Constitution. But I can tell you why the Drafting Committee has used it. The Drafting Committee wanted to make it clear that though India was to be a federation, the Federation was not the result of an agreement by the States to join in a Federation and that the Federation not being the result of an agreement no State has the right to secede from it. The Federation is a Union because it is indestructible. Though the country and the people may be divided into different States for convenience of administration the country is one integral whole, its people a single people living under a single imperiumderived from a single source. The Americans had to wage a civil war to establish that the States have no right of secession and that their Federation was indestructible. The Drafting Committee thought that it was better to make it clear at the outset rather than to leave it to speculation or to dispute.

The provisions relating to amendment of the Constitution have come in for a virulent attack at the hands of the critics of the Draft Constitution. It is said that the provisions contained in the Draft make amendment difficult. It is proposed that the Constitution should be amendable by a simple majority at least for some years. The argument is subtle and ingenious. It is said that this Constituent Assembly is not elected on adult suffrage while the future Parliament will be elected on adult suffrage and yet the former has been given the right to pass the Constitution by a simple majority while the latter has been denied the same right. It is paraded as one of the absurdities of the Draft Constitution. I must repudiate the charge because it is without foundation. To know how simple are the provisions of the Draft Constitution in respect of amending the Constitution one has only to study the provisions for amendment contained in the American and Australian Constitutions. Compared to them those contained in the Draft Constitution will be found to be the simplest. The Draft Constitution has eliminated the elaborate and difficult procedures such as a decision by a convention or a referendum. The Powers of amendment are left with the Legislature Central and Provincial. It is only for amendments of specific matters – and they are only few – that the ratification of the State legislatures is required. All other Articles of the Constitution are left to be amended by Parliament. The only limitation is that it shall be done by a majority of not less than two-thirds of the members of each House present and voting and a majority of the total membership of each House. It is difficult to conceive a simpler method of amending the Constitution.

What is said to be the absurdity of the amending provisions is founded upon a misconception of the position of the Constituent Assembly and of the future Parliament elected under the Constitution. The Constituent Assembly in making a Constitution has no partisan motive. Beyond securing a good and workable constitution it has no axe to grind. In considering the Articles of the Constitution it has no eye on getting through a particular measure. The future Parliament if it met as a Constituent Assembly, its members will be acting as partisans seeking to carry amendments to the Constitution to facilitate the passing of party measures which they have failed to get through Parliament by reason of some Article of the Constitution which has acted as an obstacle in their way Parliament will have an axe to grind while the Constituent Assembly has none. That is the difference between the Constituent Assembly and the future Parliament. That explains why the Constituent Assembly though elected on limited franchise can be trusted to pass the Constitution by simple majority and why the Parliament though elected on adult suffrage cannot be trusted with the same power to amend it.

I believe I have dealt with all the adverse criticisms that have been levelled against the Draft Constitution as settled by the Drafting Committee. I don’t think that I have left out any important comment or criticism that has been made during the last eight months during which the Constitution has been before the public. It is for the Constituent Assembly to decide whether they will accept the constitution as settled by the Drafting Committee or whether they shall alter it before passing it.

But this I would like to say. The Constitution has been discussed in some of the Provincial Assemblies of India. It was discussed in Bombay, C. P., West Bengal, Bihar, Madras and East Punjab. It is true that in some Provincial Assemblies serious objections were taken to the financial provisions of the constitution and in Madras to Article 226. But excepting this, in no Provincial Assembly was any serious objection taken to the Articles of the Constitution. No Constitution is perfect and the Drafting Committee itself is suggesting certain amendments to improve the Draft Constitution. But the debates in the Provincial Assemblies give me courage to say that the Constitution as settled by the Drafting Committee is good enough to make in this country a start with. I feel that it is workable, it is flexible and it is strong enough to hold the country together both in peace time and in war time. Indeed, if I may say so, if things go wrong under the new Constitution. The reason will not be that we had a bad Constitution. What we will have to say is, that Man was vile. Sir, I move.

Maulana Hasrat Mohani has given notice of an amendment. It was given at half-past Eleven this morning. I will allow him to move it, particularly because it will have the effect, if it is lost, of blocking another motion of which I have got notice. Maulana Sahib, will you kindly move your amendment?

*[Sir, the amendment, of which I have given notice, is to the effect that the present Constitution Assembly is not competent and there are three reasons why I do not regard it as competent. The first and the most important reason is . . . . . . . . . .]

Mr. President, Sir, will Maulana Sahib please read out the amendment first?

I will read out the amendment. The amendment is this:

“That the Consideration of the Draft Constitution of India be postponed till the election of a fresh and competent Constituent Assembly on the basis of joint electorate and the formation of political rather than communal parties in India.” That is the amendment.

May I rise on a point of order, Sir? My point of order, is that Maulana Sahib cannot move his negative amendment after ………..

Won’t you allow him to move it?

He has just spoken in Hindustani, the purport of which is that he has moved his amendment. This is contrary to the practice of this House. I think it is out of order and it should not be allowed.

I think I had better allow the Maulana Saheb to move the amendment. Then, you may take the point of order.

*[I was telling the reason why I do not regard this Constituent Assembly as a competent body. Firstly, because all over the world wherever a Constituent Assembly has been set up, it has been done as an outcome of revolution. Revolution does not necessarily mean an armed revolution. It only means that, when the prevailing system of Government has come to an end and another is intended to be set up in its place, a Constituent Assembly has been invariably called to frame and pass a constitution in the light of new conditions. If the previous form of Government were to continue then there was no need of a Constituent Assembly. Look at our new constitution drafted by Dr. Ambedkar. There is nothing new in it. He has mostly copied out either the Government of India Act of 1935 or, as admitted by himself, has drawn from the constitutions of other countries. A bit from here and a bit from there–it is a Pandora’s Box. This is what has been produced by our friend Dr. Ambedkar! My biggest complaint on this account is that if for the purpose of drafting a constitution he had to copy out the constitutions of other countries, then why did he not embody the latest and the best constitution? How was it that he looked up to the constitutions of Australia, Canada, America, and England, but the constitution of the Soviet Union did not catch his eye? I have jotted down all the points he has made in his speech. This is not the time to reply them in detail, but this much I can say that he has retained all the bad points that he could lay his hands upon. He has observed that there should be no rigidity and legalism, but has he at any place said that a Unitary System of Government should be established? At one place he mentioned that he could not provide for the village Panchayats. If he had kept the Soviet Constitution in view, there would have been no difficulty in his way. I claim it and I challenge him on that point. For example, he has said that unless there is a unitary type of Government and a powerful Centre, nothing can be done. Such talk is beside the point. He does not know that it is so in the Soviet Constitution. What he has done is to allocate some subjects to Provinces, some to the Centre and some have been put in the concurrent list. In the Soviet Constitution every constituent state has been made a permanent republic; and to win its confidence every component unit has been given control over the defence, foreign relations and communications. What has been the result? He says that it would be detrimental, but there the Soviet Government have gained the confidence of their component states. The result has been that all parts of the Soviet Union – considered from the point of view of population they are all Muslim republics – have helped their utmost in the last war. People of Caucasia and of every war-ravaged region have stood wholeheartedly by the Soviet Union. Cossacks and others who rendered help all belonged to the Union. Thus his observation is unjustified. He is not taking the people into his confidence, and says that all should merge.]

May I rise to a point of order? The revered Maulana Sahib is discussing the merits of the Constitution whereas the proposal that is put forward before us is that we must not consider this Constitution. The discussion of the merits of the Constitution cannot be brought before the House when we are to consider only the question of postponement of the discussion.

I thought it would save time if you left him alone.

*[I repeat what I have already said, that the reason why this House is not competent, is that you have consulted all the constitutions of the world; but you have not cared to see the latest and the best constitutions. The second point arises, what was the basis of the election of our Constituent Assembly? It was on communal basis. Muslims had elected Muslims and Hindus had voted for the Hindus, but the States were not represented. What was the position at the time of the first meeting of the Constituent Assembly? On your own admission there were three parties, namely, the Congress, the Muslim League and the States; but up to that time the States had not come in. No member of the Muslim League had taken any part. The result has been that the constitution that has been framed has been forged by one party alone. How can you enforce it on others? I mean to say that no reliance can be placed by us as the Constitution has been framed by one party alone. In the situation that has how arisen we also find the same, namely that there is only one party. It is like this: the Muslim League is finished, it has dissolved itself and all the States have merged themselves in the Indian Union and now only the Indian Government, namely one party, has remained in the field. That is why we have to form political parties so that your difficulties may come to an end.]

*[Did you find out any better solution?]

*[I am coming to that. Dr. Ambedkar has just said that the majority party should be considerate towards the Minority party. I say: we do not want them. You have provided in the constitution that 14 percent of the seats should be reserved for the Muslims. You still consider yourself 86 per cent and Muslims to be 14 percent. So long as you have this communalism, nothing can be done. Why do you say that Muslims are in a Minority. So long as you depict them in communal colours Muslims shall remain a Minority. When we come as members of a political party or as members of the Independent Communist party or as Socialists and then form a coalition party, then as a whole they will be arrayed against the rest.

You say that a long time has elapsed that many things have happened and that you have worked so hard. Mr. President, I would recall that when PanditJawaharLal Nehruhad presented the Draft Constitution, I had then raised an objection and he had advised me to leave alone a primary matter. I had thereupon pointed out to him that it would be absurd to leave aside a point which is to be settled first. I had also pointed out that by doing so he would not be taking any strong and firm stand but would be stuffing irrelevant matter in all directions. I had also enquired what he would do if questions were raised on these issues, if without taking any decision, he started framing the constitution. It is a futility; we should see what type of Constitution is required. We want to make a picture, but if that picture is not painted correctly, then it cannot be termed a picture. You will say that you have worked hard and that quite a long time has elapsed. My answer would be that there is no difficulty about it, neither was there any risk. I had protested at that time and I was glad that the Honourable President had stated that the point would be considered and it was on that understanding that we had discussed the resolution. You know that the same thing has happened in Pakistan as well. Mr.Jinnah had said that so long as the Constituent Assembly was not elected, the constitution could not be passed. This is the reason why I am telling you that so long as the Constituent Assembly is not elected on non-communal basis, you have no right to get a constitution passed by this Constituent Assembly. No matter receives any consideration from you, because you are inflated with the idea that you are in a majority and that whatever you like will be passed. Do not imagine that no blame will come upon you. I am alone and Ian saying all I can say. You may not agree. In reality you are doing all that the British Government had been doing. After sometime they used to give us pensions and used to ask us to stay at home. But why should we do so?

I would like to ask you what you are doing in Hyderabad. You say that a Constituent Assembly will be setup which would frame a constitution. You have accepted this principle for Hyderabad. Why don’t you do it here? Obviously all this is being done on communal lines in which truth and justice have no place.

If he says that he cannot do that, he has no power to elect a new Constituent Assembly on the basis of joint electorate and that would be done after the constitution has-been framed, then I repeat what you have said, that ‘legalism’ and ‘rigidity’ should be cast aside. I ask him whether he can set up a Constituent Assembly in Hyderabad without the Nizam’s fireman. But here we set up an electorate for the Constituent Assembly as we felt the need for it; so it is incorrect to say that we can not do it. “Where there is a will, there is a way.” If you are in earnest to be just to the country and if you want to treat every one equally, then I give you a warning that your endeavour to assimilate all into one whole, to build a paramount Indian power, will bring disaster. The latest example is that of Aurangazeb the Emperor. After conquering the whole of India he annexed the two Southern States of Bijapur and Golcanda with the intention of founding aunitary Moghul Empire. What was the result? They say Aurangazeb lost his kingdom because of his bigotry but I say it was lost because of his imperialistic ideas. If he had not done that, he would not have lost a kingdom. Do not think it is easy to form a single unitary Government by coercing each and all into your fold. That can not last. You should hold fresh elections on non-communal basis, on the basis of joint electorates, and then whatever constitution you frame will be acceptable to us. We regard the constitution framed by you worthy of being consigned to the waste paper basket.]

I wish to point out that under Rule 31 sub-clause (2) the motion for adjournment on the motion moved by the Honourable Dr. B. R. Ambedkar for the consideration of Draft Constitution of India should not have been allowed by the Chair.

I have taken this under Rule 25, Clause(5), sub-clause (b) as a motion for adjournment of consideration of a motion which is under discussion.

But he is wanting a fresh election to take place first in the country. That is a negation of the whole idea.

I have liberally construed the rule for the Honourable Member and I have taken it, as I have said, under Rule 25, Clause (5), sub-clause (b).

Sir, before we adjourn for the day, may I know how many days the Chair proposes to allow for the general discussion on Dr. Ambedkar’s motion?

As at present advised, it is hoped to conclude the discussion tomorrow. I will limit the time of each speaker and if I find that there is a considerable opinion in favour of further discussion, more time may be given.

The Constituent Assembly then adjourned till Ten of the Clock on Friday the 5th November 1948.

*[ ] Translation of Hindustani Speech